Toán cho các nhà kinh tế 2
Đề cương trắc nghiệm Toán cho các nhà kinh tế 2, Đại học kinh tế quốc dân Neu E-learning
Xem bản đầy đủ TẠI ĐÂY hoặc LIÊN HỆ
Câu hỏi 1
Cho hàm số y=5×2−4cosx+3. Đạo hàm y′ là:
Select one:
a. y′=10x+4sinx+3
b. y′=10x+4sinx
c. y′=10x−4sinx
d. y′=10x−4sinx+3
Phản hồi
Đúng. Đáp án đúng là: y′=6×2−10x+1 } { y′=6.12−10.1+1=−3. Tham khảo: Mục 2.3.1. Đạo hàm của tổng, hiệu, tích, thương các hàm số (BG, tr.21).
The correct answer is: y′=10x+4sinx
Câu hỏi 2
Cho hàm số y=(5×2−3x−1)6. y′(1) có giá trị là:
Select one:
a. 42
b. 1
c. 6
d. -42
Phản hồi
y=(5x23x1)6 có dạng hàm hợp y=u6 Theo công thức đạo hàm của hàm hợp thì: (u6)′=6.u5.u′ ^{ } Nên [(5×2−3x−1)6]′=6(5×2−3x−1)5.(5×2−3x−1)′=6(5×2−3x−1)5.(10x−3) Thay x = 1, ta có: y′(1)=42. {Tham khảo: }}Mục 2.3.2. Đạo hàm của hàm hợp (BG, tr.22).}
The correct answer is: 42
Câu hỏi 3
Cho hàm số y=sin(2x−5). Đạo hàm y′ là:
Select one:
a. y′=cos(2x−5)
b. y′=2.cos(2x−5)
c. y′=sin(2)
d. y′=2.sin(2x−5)
Phản hồi
Đúng. Đáp án đúng là: y’=2.cos(2x-5) Vì: Ở đây hàm số y = sin(2x-5) có dạng hàm hợp y = sin(u); với u = 2x- 5 ⇒ Dùng công thức (sinu)’=u^’.cos(u)⇒[sin(2x-5)]=(2x-5)’.cos(2x-5) =2.cos(2x-5) Tham khảo: Mục 2.3.2. Đạo hàm của hàm hợp (BG, tr.22).
The correct answer is: y′=2.cos(2x−5)
Câu hỏi 4
Biểu thức vi phân của hàm y=x2.e−5x là
Select one:
a. dy=−5×2.e−5x.dx
b. dy=2x.e−5x.dx
c. dy=−10x.e−5x.dx
d. dy=(2x−5×2)e−5x.dx
Phản hồi
The correct answer is: dy=(2x−5×2)e−5x.dx
Câu hỏi 5
Cho hàm số y=ln(2×2−5x+8). Tập xác định của hàm số là:
Select one:
a. (−∞,2]
b. (2,+∞)
c. R
d. [2,+∞)
Phản hồi
The correct answer is: R
Câu hỏi 6
Cho hàm số y=2x+1√x+1. Giá trị y′(1) là:
Select one:
a. c
b. d
c. b
d. a
Phản hồi
The correct answer is: a
Câu hỏi 7
Select one:
a. a
b. d
c. c
d. b
Phản hồi
The correct answer is: a
Câu hỏi 8
PNG204
Select one:
a. y′(e2)=3e
b. y′(e2)=3
c. y′(e2)=6e
d. y′(e2)=−6e
Phản hồi
The correct answer is: y′(e2)=6e
Câu hỏi 9
Cho hàm số y=ln(2x−37−4x). Đạo hàm y′ có giá trị là:
PNG210
Select one:
a. c
b. b
c. d
d. a
Phản hồi
The correct answer is: b
Câu hỏi 10
y=sin(2x−1−−−−−−√) . Đạo hàm y′ là:
Select one:
a. y′=sin(12x−1√)
b. y′=12x−1√⋅cos(2x−1−−−−−−√)
c. y′=cos(12x−1√)
d. y′=cos(2x−1−−−−−−√)
Phản hồi
The correct answer is: y′=12x−1√⋅cos(2x−1−−−−−−√)
Câu hỏi 11
Cho hàm số y=e−2×3+5×2−4x+1 . Số điểm cực trị của hàm số là:
Select one:
a. 1
b. 4
c. 2
d. 3
Phản hồi
The correct answer is: 2
Câu hỏi 12
Cho hàm số y=∛x. Số điểm tới hạn của hàm số là:
Select one:
a. 4
b. 1
c. 2
d. 3
Phản hồi
Đúng. Đáp án đúng là: 1 Vì: y^’=1/(3∛(x^2 )) y’ không xác định tại x = 0 Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).
The correct answer is: 1
Câu hỏi 13
Cho hàm số y=x2lnx. Điểm cực trị của hàm số là:
Select one:
a. e
b. 1
c. 0
d. e−1/2
Phản hồi
Vì: TXĐ: (0,+∞) } y′=2xlnx+x=x(2lnx+1) { } y′=0⇒2lnx=−1⇒x=e−1/2. y′′=2lnx+3;y′′(e−1/2)=2>0. {Hàm số đạt cực tiểu tại x=e−1/2. } {{Tham khảo: }}}{Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33)
The correct answer is: e−1/2
Câu hỏi 14
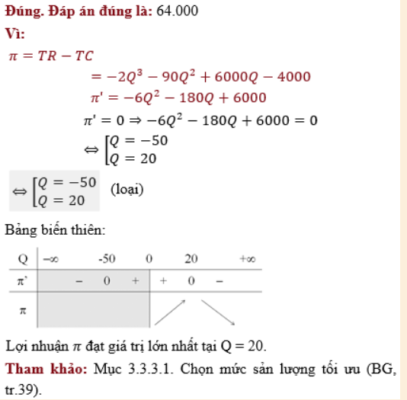
Giả sử doanh thu và chi phí của một nhà sản xuất được cho tương ứng bởi: TR=−70Q2+5000QTC=2Q3+20Q2−1000Q+4000 Lợi nhuận tối đa của doanh nghiệp là:
Select one:
a. 64.000
b. 40.000
c. 32.000
d. 30.000
Phản hồi
The correct answer is: 64.000
Câu hỏi 15
Giả sử doanh nghiệp độc quyền sản xuất một loại sản phẩm với hàm cầu là p=300-2Q. Doanh thu cận biên tại mức sản lượng Q = 9 là:
Select one:
a. 260
b. 264
c. 282
d. 276
Phản hồi
Vì: TR=p.Q=(300−2Q)Q=−2Q2+300Q ⇒TR′=−4Q+300⇒TR′(9)=264 }} {Tham khảo: }}Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36)
The correct answer is: 264
Câu hỏi 16
Theo quy luật lợi ích cận biên giảm dần, hàm sản xuất Q=f(K,L) sẽ phải thỏa mãn điều kiện:
Select one:
a. Q′′KK≤0;Q′′LL≥0, ∀K,L>0
b. Q′′KK≤0;Q′′LL≤0, ∀K,L>0
c. Q′′LK≤0;Q′′KL≤0, ∀K,L>0
d. Q′′KK≤0;Q′′KL≤0, ∀K,L>0
Phản hồi
{Đúng. Đáp án đúng là}}: Q′′KK≤0;Q′′LL≤0, ∀K,L>0 {Vì: }}Theo quy luật lợi ích cận biên giảm dần các đạo hàm riêng cấp 2 theo cùng 1 biến số phải âm. {Tham khảo: }}Mục 4.7.2. Đạo hàm riêng cấp 2 và quy luật lợi ích cận biên giảm dần (BG, tr. 55). }
The correct answer is: Q′′KK≤0;Q′′LL≤0, ∀K,L>0
Câu hỏi 17
Điểm (2, –1) thuộc miền xác định của hàm số:
Select one:
a. 1−3x−y−−−−−−−−−√
b. w=y+2xx+2y
c. w=ln(y2−x)
d. w=exy
Phản hồi
Đúng. Đáp án đúng là: w=e^xy Vì: Thay x = 2, y = –1 vào các biểu thức chỉ biểu thức của đáp án B xác định giá trị Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).
The correct answer is: w=exy
Câu hỏi 18
Hàm số 2 biến số w=f(x,y) có số đạo hàm riêng cấp 2 nhiều nhất là:
Select one:
a. 6
b. 4
c. 2
d. 8
Phản hồi
{Đúng. Đáp án đúng là}}: 4 {Vì:} }Hàm số 2 biến số {có thể có} 4 đạo hàm riêng cấp 2 là w”xx, w”xy, w”yx, w”yy {Tham khảo:} }Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).
The correct answer is: 4
Câu hỏi 19
Điểm (1, –2) thuộc miền xác định của hàm số:
Select one:
a. 1+3x+y−−−−−−−−−√
b. w=ln(x2+y)
c. w=1−3x+2y2x+y
d. w=x+2y−−−−−−√
Phản hồi
Đúng. Đáp án đúng là: √(1+3x+y) Vì: Thay x = 1, y = –2 vào các biểu thức chỉ biểu thức của đáp án D xác định giá trị Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).
The correct answer is: 1+3x+y−−−−−−−−−√
Câu hỏi 20
Biểu thức vi phân toàn phần của hàm số w=sin(3x−2y) là:
Select one:
a. dw=3sin(3x−2y)dx−2sin(3x−2y)dy
b. dw=cos(3x−2y)dx+cos(3x−2y)dy
c. dw=3.cos(3x−2y)dx+2.cos(3x−2y) dy
d. dw=3.cos(3x−2y)dx−2cos(3x−2y) dy
Phản hồi
Đúng. Đáp án đúng là: dw=3.cos(3x−2y)dx−2cos(3x−2y) {Vì:} w′x=3cos(3x−2y),w′y=−2cos(3x−2y) } Lập theo công thức của biểu thức vi phân. Tham khảo: Mục 4.5. Vi phân (BG, tr. 52).}
The correct answer is: dw=3.cos(3x−2y)dx−2cos(3x−2y) dy
Câu hỏi 21
Xét hàm số 2 biến số w=f(x,y) có các đạo hàm riêng: w′x=−2x−2y−3;w′y=−2x−6y+1 . Biết rằng điểm M0(−52,1) là điểm dừng của hàm số, khi đó điểm dừng M0 :
Select one:
a. là điểm cực tiểu của hàm số.
b. không là điểm cực trị của hàm số.
c. là điểm cực đại của hàm số.
d. có thể là điểm cực đại hoặc điểm cực tiểu của hàm số .
Phản hồi
The correct answer is: là điểm cực đại của hàm số.
Câu hỏi 22
Xét bài toán tìm cực trị của hàm số w=x.y với điều kiện 3x−y=5 . Khi sử dụng phương pháp nhân tử Lagrange, hàm Lagrange là:
Select one:
a. L=5−3x+y−λx.y
b. L=3x−y+λ(5−x.y)
c. L=x.y+λ(5−3x−y)
d. L=x.y+λ(5−3x+y)
Phản hồi
{Đúng. Đáp án đúng là: L=x.y+λ(5−3x+y) }} {Vì: }}Hàm x.y là hàm Mục tiêu, phương trình ràng buộc là 3x−y=5 . {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}
The correct answer is: L=x.y+λ(5−3x+y)
Câu hỏi 23
Hàm số w=x2−y2+3x−2y có điểm dừng là:
Select one:
a. M0(32;1)
b. M0(−32;12)
c. M0(3;−1)
d. M0(−32;−1)
Phản hồi
The correct answer is: M0(−32;−1)
Câu hỏi 24
Hàm số w=3×2+y2−3x−2y có điểm dừng là:
Select one:
a. M0(2;1)
b. M0(−12;1)
c. M0(1;1)
d. M0(12;1)
Phản hồi
The correct answer is: M0(12;1)
Câu hỏi 25
Hàm số w=f(x, y) có các đạo hàm riêng là w′x=2mx+y−3;w′y=x−5 trong đó m là tham số. Điểm M0(5,−1) là điểm dừng của hàm số w khi m có giá trị là:
Select one:
a. −5
b. 5
c. 5/2
d. 2/5
Phản hồi
{Đúng. Đáp án đúng là: 2/5 }} {Vì: }}Thay x=5,y=−1 , tìm m để 2 đạo hàm riêng đều triệt tiêu. 2.5.m+(−1)−3=05−5=0⇔m=25 {Tham khảo: }}Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).}
The correct answer is: 2/5
Câu hỏi 26
Tính tích phân: I=∫2sin2x2⋅dx
Select one:
a. x+sinx+C
b. x+cosx+C
c. x-cosx+C
d. x-sinx+C
Phản hồi
Đúng. Đáp án đúng là: x−sinx+C }} {Vì: }}Sử dụng công thức lượng giác, sau đó áp dụng công thức tích phân cơ bản. I=∫2sin2x2⋅dx=∫(1−cosx).dx=x−sinx+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)
The correct answer is: x-sinx+C
Câu hỏi 27
Tính tích phân: ∫dx1−cos2x
Select one:
a. 12cotx+C
b. −12cotx+C
c. cotx+C
d. −cotx+C
Phản hồi
{Đúng. Đáp án đúng là: −12cotx+C }} {Vì: }}Áp dụng công thức tích phân cơ bản để ra kết quả ∫dx1−cos2x=∫dx2sin2x=−12⋅cotx+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)}
The correct answer is: −12cotx+C
Câu hỏi 28
Tinh tích phân:
∫ex⋅dxex+1
Select one:
a. −ln(ex+1)+C
b. ln(ex+1)+C
c. 2ln(ex+1)+C
d. −2ln(ex+1)+C
Phản hồi
Đúng. Đáp án đúng là: ln(ex+1)+C }} {Vì:}} { ∫ex⋅dxex+1=∫d(ex+1)ex+1=ln(ex+1)+C }} {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74
The correct answer is: ln(ex+1)+C
Câu hỏi 29
Tính tích phân:I = ∫dxsinx
Select one:
a. ln|tanx2|+C
b. −ln|cotx2|+C
c. ln|cotx2|+C
d. −ln|tanx2|+C
Phản hồi
The correct answer is: ln|tanx2|+C
Câu hỏi 30
Tính tích phân:
I=∫x.ex(x+1)2dx
Select one:
a. b
b. a
c. c
d. d
Phản hồi
The correct answer is: c
Câu hỏi 31
PNG716
Select one:
a. π/4
b. π
c. π/2
d. π/3
Phản hồi
The correct answer is: π/4
Câu hỏi 32
PNG709
Select one:
a. 4√2
b. 4√3
c. 3√2
d. 5√2
Phản hồi
The correct answer is: 4√2
Câu hỏi 33
PNG713
Select one:
a. ln2+12
b. ln3+12
c. ln3−12
d. ln2−12
Phản hồi
The correct answers are: ln2−12, ln3+12
Câu hỏi 34
PNG711
Select one:
a. 3/13
b. 4/15
c. 1/9
d. 2/11
Phản hồi
The correct answer is: 4/15
Câu hỏi 35
PNG701
Select one:
a. – 34
b. – 14
c. – 2
d. 2
Phản hồi
The correct answer is: – 2
Câu hỏi 36
Giả sử một doanh nghiệp có hàm doanh thu và hàm chi phí được cho bởi: TR=20Q+3Q2TC=Q2+10Q+5. Lợi nhuận của doanh nghiệp khi sản xuất Q=20 sản phẩm là:
Select one:
a. 2205
b. 1600
c. 995
d. 605
Phản hồi
Đúng. Đáp án đúng là: 995 Vì: Giá trị TR(20) = 1600, TC(20) = 605. Suy ra lợi nhuận = TR – TC = 995 Tham khảo: Mục 1.7.3. Hàm doanh thu, hàm chi phí và hàm lợi nhuận (BG, tr.13).
The correct answer is: 995
Câu hỏi 37
Cho hàm số y=x−1−−−−−√⋅3−x−−−−−√+x2−4x+3−−−−−−−−−−√ Tập xác định của hàm số là:
Select one:
a. {1,3}
b. (-∞,1∪3,+∞)
c. R
d. [1,3]
Phản hồi
The correct answer is: {1,3}
Câu hỏi 38
PNG117
Select one:
a. 0,2e
b. 0,1e
c. 0,3e
d. 1,5e
Phản hồi
The correct answer is: 0,2e
Câu hỏi 39
Cho hàm số y=2x−34−x. Đạo hàm cấp hai y″ là:
Select one:
a. y”=−4(4−x)2
b. y”=10(4−x)3
c. y”=−10(4−x)3
d. y”=−58−2x
Phản hồi
The correct answer is: y”=10(4−x)3
Câu hỏi 40
Cho hàm số y=−3×2+4x−1−−−−−−−−−−−−√. Tập xác định của hàm số là:
Select one:
a. [1,+∞)
b. [13,1]
c. (−∞,13]
d. [13,+∞)
Phản hồi
The correct answer is: [13,1]
Câu hỏi 41
y=(3x−2).e−2x Giá trị của y′′(1) là: }
Select one:
a. y”(1)=8e2
b. y”(1)=−7e2
c. y”(1)=−8e−2
d. y”(1)=−8e2
Phản hồi
The correct answer is: y”(1)=−8e−2
Câu hỏi 42
Đạo hàm của y=(2x−1).tan(1−4x) là:
Select one:
a. y′=2tan(1−4x) −4(2x−1)cos2(1−4x)
b. y′=2x−1cos2(1−4x)
c. y′=2tan(1−4x) +2x−1cos2(1−4x)
d. y′=−8cos2(1−4x)
Phản hồi
The correct answer is: y′=2tan(1−4x) −4(2x−1)cos2(1−4x)
Câu hỏi 43
Cho y=ex√. Đạo hàm cấp 2 của y là:
PNG218
Select one:
a. b
b. c
c. a
d. d
Phản hồi
The correct answer is: c
Câu hỏi 44
Cho hàm số y=sin(cosx). Đạo hàm y′ là:
Select one:
a. y′=cos(cosx)
b. y′=−sinxsin(cosx)
c. y′=sin(−cosx)
d. y′=−sinxcos(cosx)
Phản hồi
Đúng. Đáp án đúng là: y′=−\sinx.cos(cosx) Vì: Đây là đạo hàm hàm hợp: (sinu)′=u′.cosu. Tham khảo: Mục 2.3.2. Đạo hàm của hàm hợp (BG, tr.22).
The correct answer is: y′=−sinxcos(cosx)
Câu hỏi 45
Đạo hàm của y=x2.3x−1−−−−−−√ là:
Select one:
a. y′=15×2−4x23x−1√
b. y′=3x3x−1√
c. y′=9×2−2x23x−1√
d. y′=23x−1−−−−−−√
Phản hồi
The correct answer is: y′=15×2−4x23x−1√
Câu hỏi 46
Cho hàm số y=−4×2+7x−3−−−−−−−−−−−−√ . Giá trị lớn nhất của hàm số là:
Select one:
a. 0
b. 1
c. 1/2
d. 1/4
Phản hồi
The correct answer is: 1/4
Câu hỏi 47
Cho hàm số y=(−3x+5).e2x2−x+1. Hàm số tăng trên:
Select one:
a. (−23−145√24,−23+145√24)
b. (−∞,−23−145√24) và (−23+145√24,+∞)
c. (23−145√24,23+145√24)
d. (−∞,23−145√24) và (23+145√24,+∞)
Phản hồi
The correct answer is: (23−145√24,23+145√24)
Câu hỏi 48
Cho hàm(x2−3x+2).e−2x. Hàm số giảm trên:
Select one:
a. (2+12√,+∞)
b. 2 khoảng (−∞,2−12√) và (2+12√,+∞)
c. (−∞,2−12√)∪(2+12√,+∞)
d. (2−12√,2+12√)
Phản hồi
The correct answer is: (−∞,2−12√)∪(2+12√,+∞)
Câu hỏi 49
Cho hàm số y=x.ln2x. Số điểm dừng của hàm số là:
Select one:
a. 3
b. 1
c. 4
d. 2
Phản hồi
Đúng. Đáp án đúng là: 1 Vì: y’=ln2 x+1 Giải y’ = 0 ta được y’=0⇒ln2 x+1=0⇔ln2 x=-1 ⇔2x=e^(-1)⇔x=1/2e → Hàm số có 1 điểm dừng. Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).
The correct answer is: 1
Câu hỏi 50
Cho hàm số y=(x2−5x+4)10. Hàm số tăng trên:
Select one:
a. (1,52) và (4,+∞)
b. (−∞,1) và (52,4)
c. (1,4)
d. (−∞,1) và (4,+∞)
Phản hồi
The correct answer is: (1,52) và (4,+∞)
Câu hỏi 51
Đường mức của hàm số w=x^2+3y^2-x ứng với mức w0 = 1 có phương trình là:
Select one:
a. x^2+3y^2-x=0
b. x^2+3y^2-x=2
c. x^2+3y^2-x=1
d. x^2+3y^2-x=-1
Phản hồi
Đúng. Đáp án đúng là: x^2+3y^2-x=1 Vì: Cho w = w0 Tham khảo: Mục 4.1.5. Đường mức (BG, tr. 48).
The correct answer is: x^2+3y^2-x=1
Câu hỏi 52
Giá trị của hàm số w=x2+2xy−3y2 tại điểm (1, –1) là:
Select one:
a. –4
b. 0
c. 6
d. 4
Phản hồi
Đúng. Đáp án đúng là: –4 Vì: Thay x = 1, y = –1 vào biểu thức ta tính được giá trị của hàm số: 12+2.1.(−1)−3.(−1)2=−4 Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).
The correct answer is: –4
Câu hỏi 53
Đạo hàm riêng theo biến y của hàm số w=4×2+3xy−y3 tại điểm (1,2) là:
Select one:
a. 10
b. 9
c. –9
d. 14
Phản hồi
Đúng. Đáp án đúng là: –9 Vì: Lấy đạo hàm của hàm số theo biến y rồi thay x = 1, y = 2 vào tìm giá trị: w′y=3x−3y2; w′y(1,2)=3.1−3.22=−9. Tham khảo: Mục 4.4.1. Đạo hàm riêng tại một điểm (BG, tr. 51).
The correct answer is: –9
Câu hỏi 54
Đạo hàm riêng theo biến y của hàm số w=x23x−2y là:
Select one:
a. w′y=2×2(3x−2y)2
b. w′y=2x23x−2y
c. w′y=−2x2y(3x−2y)2
d. w′y=2x(3x−2y)−3×2(3x−2y)2
Phản hồi
{Đúng. Đáp án đúng là}}: w′y=2×2(3x−2y)2 {Vì:} }Lấy đạo hàm của hàm số theo biến y coi biến số x là hằng số: w′y=−x2(3x−2y)′y(3x−2y)2=2x2y(3x−2y)2 {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).}
The correct answer is: w′y=2×2(3x−2y)2
Câu hỏi 55
Với hàm sản xuất dạng Cobb – Douglas Q=a.Kα Lβ(a, α, β>0) , theo quy luật lợi ích cận biên giảm dần các tham số α, β phải thỏa mãn điều kiện:
Select one:
a. α≤1,β≤1
b. α≤0,β≤0
c. α≥0,β≥0
d. α≥1,β≥1
Phản hồi
{Đúng. Đáp án đúng là}}: α≤1, β≤1 {Vì: Q′′KK=a.α.(α−1)Kα−2Lβ≤0; }} {\fontsize{14pt}{16.8pt}\selectfont Q′′LL=a.β(β−1)KαLβ−2 ≤0 } {Tham khảo: }}Mục 4.7.2. Đạo hàm riêng cấp 2 và quy luật lợi ích cận biên giảm dần (BG, tr. 55).}
The correct answer is: α≤1,β≤1
Câu hỏi 56
Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3×2+y2=28 . Hàm Lagrange L=3x+2y+λ(28−3×2−y2) có các đạo hàm riêng cấp 1 L′x=3−6λx;L′y=2−2λy. Hàm số L có điểm dừng là M0(x0,y0,λ0) với λ0=−14 và:
Select one:
a. x_0=4;y_0=2
b. x_0=2;y_0=4
c. x_0=-2;y_0=-4
d. x_0=-4;y_0=-2
Phản hồi
{Đúng. Đáp án đúng là: x0=−2;y0=−4 }} {Vì: }}Thay λ=−14 vào phương trình L′y=0 tìm y, thay vào phương trình L′x=0 tìm x. Ta có: 3−6.(−14)x=0⇒x=−22−2.(−14)y=0⇒y=−4 {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}
The correct answer is: x_0=-2;y_0=-4
Câu hỏi 57
Sử dụng phương pháp nhân tử Lagrange giải bài toán tìm cực trị có điều kiện, ta biết rằng hàm Lagrange L có điểm dừng M0(x0,y0,−12) và L′′xx=−2λ;L′′xy=L′′yx=0;L′′yy=−4λ;g′x=3;g′y=1 . Khi đó tại điểm (x0,y0), hàm số với điều kiện đã cho:
Select one:
a. đạt giá trị cực đại.
b. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của x_0,y_0.
c. không đạt cực trị.
d. đạt giá trị cực tiểu.
Phản hồi
The correct answer is: đạt giá trị cực tiểu.
Câu hỏi 58
PNG513
Select one:
a. không là điểm cực trị của hàm số.
b. là điểm cực đại của hàm số.
c. là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a_11.
d. là điểm cực tiểu của hàm số.
Phản hồi
Đúng. Đáp án đúng là: không là điểm cực trị của hàm số.Vì: Theo điều kiện đủ của cực trị. Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị (BG, tr.60).
The correct answer is: không là điểm cực trị của hàm số.
Câu hỏi 59
Khi giải bài toán tìm cực trị của hàm số w=x2+y2 với điều kiện ràng buộc là phương trình 3x+2y=26 , hàm Lagrange L có điểm dừng là M0(x0,y0,λ0) với y0=λ0=4 và x0 có giá trị là:
Select one:
a. 6
b. 4
c. 3/2
d. 2
Phản hồi
Đúng. Đáp án đúng là: 6 Vì: Thay y = 4 vào phương trình ràng buộc tìm x. Ta có: 3x + 2.4 = 26 → x = 6 Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).
The correct answer is: 6
Câu hỏi 60
Tính tích phân: ∫sin3x⋅cos2x⋅dx
Select one:
a. cos5x5+cos3x3+C
b. cos5x5−cos3x3+C
c. sin5x5+sin3x3+C
d. sin5x5−sin3x3+C
Phản hồi
The correct answer is: cos5x5−cos3x3+C
Câu hỏi 61
Kết quả đúng của tích phân: I=∫(x2+x+1).lnx.dx
Select one:
a. (x33−x22+x)⋅lnx+(x39+x24+x)+C
b. (x33−x22−x)⋅lnx+(x39+x24+x)+C
c. (x33+x22+x)⋅lnx+(x39+x24+x)+C
d. (x33+x22+x)⋅lnx−(x39+x24+x)+C
Phản hồi
The correct answer is: (x33+x22+x)⋅lnx−(x39+x24+x)+C
Câu hỏi 62
Tính tích phân: ∫ex⋅sinx⋅dx
Select one:
a. ex⋅(sinx−cosx)2+C
b. −ex⋅(sinx+cosx)2+C
c. ex⋅(sinx+cosx)2+C
d. ex⋅(cosx−sinx)2+C
Phản hồi
The correct answer is: ex⋅(sinx−cosx)2+C
Câu hỏi 63
Tính tích phân: ∫(x2+1)3⋅dx
Select one:
a. x77+3⋅x55+x3+x+C
b. −x77+3⋅x55−x3+x+C
c. x77+3⋅x55+x3+C
d. x77−3⋅x55+x3−x+C
Phản hồi
Đúng. Đáp án đúng là: x77+3⋅x55+x3+x+C }} {Vì: }}Sử dụng công thức tích phân cơ bản ∫(x2+1)3⋅dx=∫(x6+3×4+3×2+1)dx =x77+3⋅x55+x3+x+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)
The correct answer is: x77+3⋅x55+x3+x+C


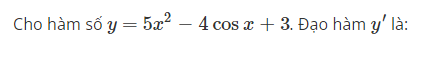


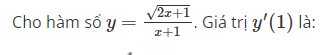
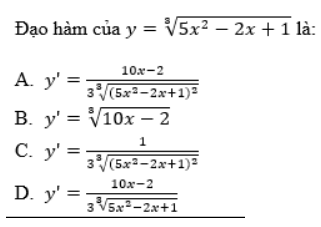
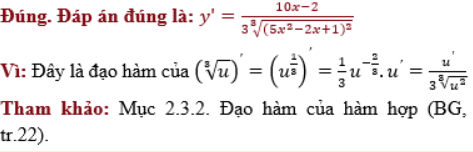
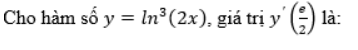

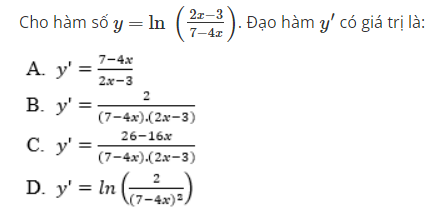
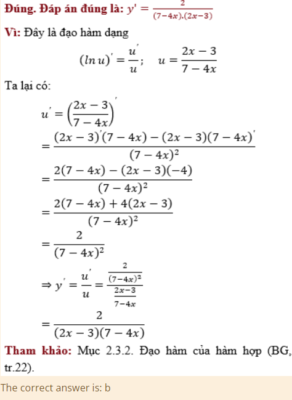
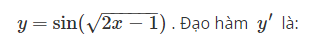




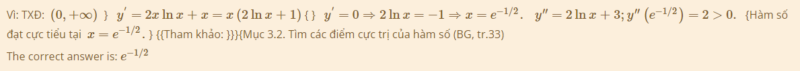





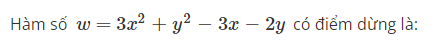

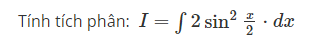

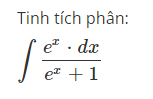
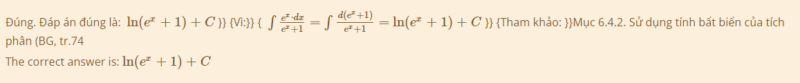



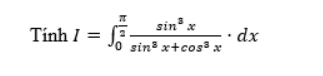

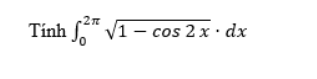

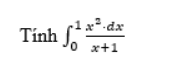

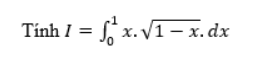

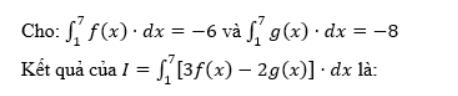

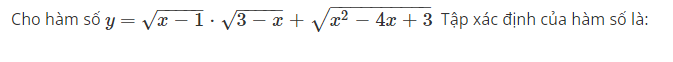

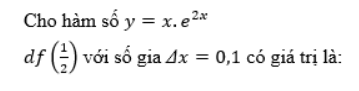

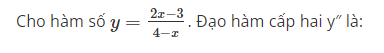
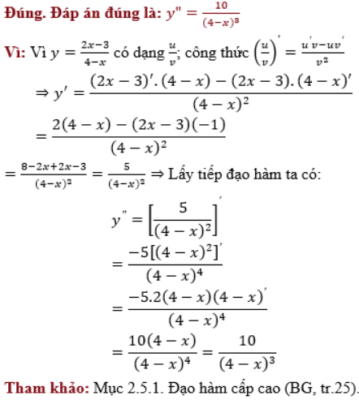
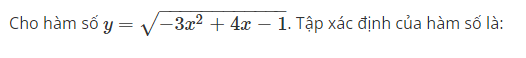




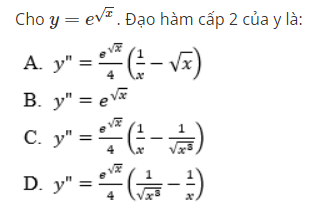
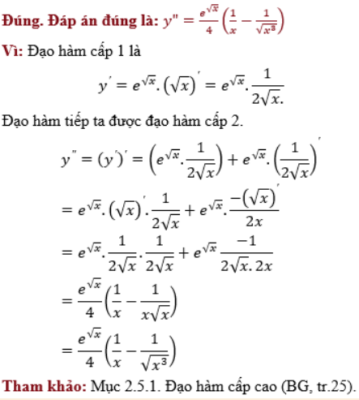
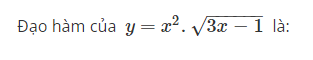

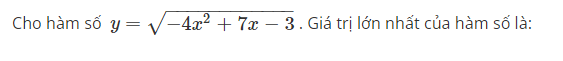


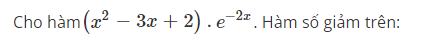

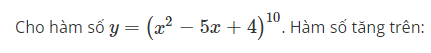

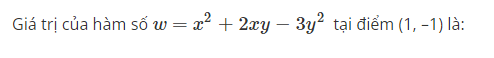
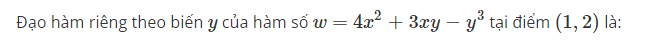





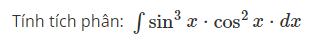



Trả lời