Toán cho các nhà kinh tế 1 (3TC)

25 Tháng Hai, 2022

admin

Please follow and like us:

Trắc nghiệm Toán cho các nhà kinh tế 1 (3TC)

Xem bản đầy đủ TẠI ĐÂY hoặc LIÊN HỆ

Cách tìm đáp án làm bài kiếm tra, bài tập.

Có thể tìm kiếm theo tên file ảnh.

Đề bài cho ảnh thì làm như sau:
+ Cách 1: Chỉ chuột vào ảnh của bài tập nhấn chuột phải hấn chuột trái vào dòng Create OR Code for this image . Khi đó xuất hiện Scan OR Code ở bên dưới có dòng mã code Ví dụ nhìn thấy phía dưới cuối dòng có C715.PNG thì đó là số C715 chuyển sang file này nhấn Crtl+ F sau đó đánh sô c715 rồi Enter đến bài có mã c715). Hoặc nhìn thấy phía dưới cuối dòng có g115.PNG thì đó là số g115 chuyển sang file này nhấn Crtl+ F sau đó đánh sô g115 rồi Enter đến bài có mã g115).

+ Cách 2: Hoặc chỉ chuột vào ảnh bài tập nhấp chuột phải, nhấp chuột trái mở trong tab mới ( dòng trên cùng cửa sổ) nhìn tên file ảnh. Sau đó tìm kiếm tên file ảnh trên file này ( ví dụ nhìn thấy tên file c715 thì tại file này nhấn Crtl+ F sau đó đánh sô c715 rồi Enter đến bài có mã c715).

Ghi chú: Trưởng hợp dùng mã file ảnh vẫn không thấy ( thỉnh thoảng có bài không có mã file ảnh), thì bôi đen 1 đáp án ( nên chọn đáp án dài nhất, không bôi đen phần a,b,c,d ở phía trước) ở bài tập rồi nhấn Ctrl+ C, chuyển sang file này nhấn Ctrl+ F, nhấn Ctrl+ V rồi Enter đến bài cần tìm.

Những bài không phải file ảnh.

Bôi đen câu hỏi hoặc 1 đáp án ( nên chọn đáp án dài nhất, không bôi đen phần a,b,c,d ở phía trước) ở bài tập rồi nhấn Ctrl+ C, chuyển sang file này nhấn Ctrl+ F, nhấn Ctrl+ V rồi Enter đến bài cần tìm.

Cho hàm số y=2x−34−x. Đạo hàm cấp hai y″ là:

Select one:
a. y”=10(4−x)3
b. y”=−4(4−x)2
c. y”=−58−2x
d. y”=−10(4−x)3
Phản hồi
3TCg119

The correct answer is: y”=10(4−x)3

Cho hàm số y=(3×3−5x+1).sinx. Đạo hàm y′ là:

Select one:
a. y′=(9×2−5)sinx
b. y′=(9×2−5)sinx+(3×3−5x+1)cosx
c. y′=(9×2−5)cosx
d. y′=(3×3−5x+1)cosx
Phản hồi
Đúng. Đáp án đúng là:y′=(9×2−5)sinx+(3×3−5x+1)cosx }} {Vì: }}Đây là đạo hàm tích u.v với u=(3×3−5x+1);v=sinx ⇒y′=(3×3−5x+1)′sinx++(3×3−5x+1)(sinx)′ =(9×2−5)sinx+(3×3−5x+1)cosx⇒ Đáp án B Tham khảo: Mục 2.3.1. Đạo hàm của tổng, hiệu, tích, thương các hàm số (BG, tr.21).

The correct answer is: y′=(9×2−5)sinx+(3×3−5x+1)cosx

3TCc106

Select one:
a. 74
b. −54
c. e−1/2−1
d. 3−63√4
Phản hồi
Đúng. Đáp án đúng là: −54 }} {Vì: cos(−π3)=12,y(12)=(12)2−32=−54 Tham khảo: Mục 1.2.2. Hàm số cho dưới dạng biểu thức (BG, tr.4) và mục 1.6.2. Các phép toán sơ cấp đối với hàm số (BG, tr. 11).

The correct answer is: −54

Cho hàm số y=ln(2×2−5x+8). Tập xác định của hàm số là:

Select one:
a. [2,+∞)
b. (2,+∞)
c. R
d. (−∞,2] Phản hồi
3TCg102

The correct answer is: R

Cho hàm số y=2x+1√x+1. Giá trị y′(1) là:

Select one:
a. a
b. b
c. c
d. d
Phản hồi

3TCg214

The correct answer is: a

Cho hàm số y=x−−√.sin2x Khi đó y′(π4) là:

Select one:
a. y′(π4)=1
b. y′(π4)=1π√
c. y′(π4)=2π−−√
d. y′(π4)=2π−−√
Phản hồi

3TCg2020

The correct answer is: y′(π4)=1π√

3TCc204

Select one:
a. y′(e2)=−6e
b. y′(e2)=3
c. y′(e2)=6e
d. y′(e2)=3e
Phản hồi

3TCg204

The correct answer is: y′(e2)=6e

Cho hàm số y=sin(cosx). Đạo hàm y′ là:

Select one:
a. y′=sin(−cosx)
b. y′=cos(cosx)
c. y′=−sinxsin(cosx)
d. y′=−sinxcos(cosx)
Phản hồi
Đúng. Đáp án đúng là: y′=−\sinx.cos(cosx) Vì: Đây là đạo hàm hàm hợp: (sinu)′=u′.cosu. Tham khảo: Mục 2.3.2. Đạo hàm của hàm hợp (BG, tr.22).

The correct answer is: y′=−sinxcos(cosx)

Cho y=e^√x. Đạo hàm cấp 2 của y là:

3TCp218

Select one:
a. a
b. b
c. c
d. d
Phản hồi

3TCg218

The correct answer is: c

Đạo hàm của hàm số y=tan3(6x) là:

Select one:
a. y′=3tan2(6x)cos2(6x)
b. y′=3tan2(6x)
c. y′=6cos2(6x)
d. y′=18tan2(6x)cos2(6x)
Phản hồi

3TCg207

The correct answer is: y′=18tan2(6x)cos2(6x)

Cho $y = (x^2 + e^x)^x$. Đạo hàm $y’$ là:

3TCp216

Select one:

a. a
b. b
c. c
d. d
Phản hồi
3TCg216

The correct answer is: a

Cho hàm số y=ln(2x−37−4x). Đạo hàm y′ có giá trị là:

3TCp210

Select one:
a. a
b. b
c. c
d. d
Phản hồi

3TCg210

The correct answer is: b

Cho hàm số y=−3×2+4x−1−−−−−−−−−−−−√. Tập xác định của hàm số là:

Select one:
a. [13,1] b. [13,+∞)
c. [1,+∞)
d. (−∞,13] Phản hồi

3TCg101

The correct answer is: [13,1]

Cho hàm f(x)=x−−√,g(x)=ex(x−1). Đạo hàm của hàm h(x)=g(f(x)) là:

3TCp217

Select one:
a. a
b. b
c. c
d. d
Phản hồi

3TCg217

The correct answer is: d

y=(3x−2).e−2x Giá trị của y′′(1) là: }

Select one:
a. y”(1)=−8e2
b. y”(1)=−7e2
c. y”(1)=−8e−2
d. y”(1)=8e2
Phản hồi
3TCg201

The correct answer is: y”(1)=−8e−2

Cho hàm số y=2x+1√x+1. Giá trị y′(1) là:

3TCp214

Select one:
a. a
b. b
c. c
d. d
Phản hồi

The correct answer is: a

Giả sử một doanh nghiệp có hàm sản xuất là Q=20L−−√ . Sản phẩm hiện vật cận biên của lao động tại mức L = 9 (đơn vị lao động) là:

Select one:
a. 60
b. 20
c. 10/3
d. 20/3
Phản hồi
Đúng. Đáp án đúng là: 10/3 Vì: Q’=20/(2√L)=10/√L ⇒Q’ (9)=10/3 Tham khảo: Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36).

The correct answer is: 10/3

3TCc323

Select one:
a. 10.000.000
b. 1.000.000
c. 100.000
d. 10.000
Phản hồi

3TCg323

The correct answer is: 10.000.000

Cho hàm số y=x.e−3×2 . Số điểm cực tiểu của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
3TCg306

The correct answer is: 1

Cho hàm số y=(−3x+5).e2x2−x+1. Hàm số tăng trên:

Select one:
a. (23−145√24,23+145√24)
b. (−23−145√24,−23+145√24)
c. (−∞,23−145√24) và (23+145√24,+∞)
d. (−∞,−23−145√24) và (−23+145√24,+∞)
Phản hồi
3TCg310

The correct answer is: (23−145√24,23+145√24)

Cho hàm số y=x−−√.e−2x . Khoảng tăng của hàm số là:

Select one:
a. R
b. (0,14)
c. (14,+∞)
d. (0,+∞)
Phản hồi
3TCg327

The correct answer is: (0,14)

Cho hàm số y=x.ln2x. Số điểm dừng của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
Đúng. Đáp án đúng là: 1 Vì: y’=ln⁡2 x+1 Giải y’ = 0 ta được y’=0⇒ln⁡2 x+1=0⇔ln⁡2 x=-1 ⇔2x=e^(-1)⇔x=1/2e → Hàm số có 1 điểm dừng. Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 1

Cho hàm số y=(5×2−7x+2)2014. Số điểm cực trị của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
3TCg305

The correct answer is: 3

Biểu thức vi phân toàn phần của hàm số w=lnxy là:

Select one:
a. dw=ydx+lnx dy
b. dw=1xdx−1y dy
c. dw=1xydx−1y2dy
d. dw=1xydx−lnxy2dy
Phản hồi
{Đúng. Đáp án đúng là}}: dw=1xydx−lnxy2dy {Vì:} w′x=1xy;w′y=−lnxy2 } Lập theo công thức của biểu thức vi phân. {Tham khảo:} }Mục 4.5. Vi phân (BG, tr. 52).}

The correct answer is: dw=1xydx−lnxy2dy

Đạo hàm riêng theo biến y của hàm số w=x^3+xy^2-3x+y là:
Select one:
a. 3x^2-3
b. 3x^2+y^2-2
c. 3x^2+y^2-3
d. 2xy+1
Phản hồi
Đúng. Đáp án đúng là: 2xy+1 Vì: Lấy đạo hàm của hàm số theo biến y. Tham khảo: Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).

The correct answer is: 2xy+1

Miền xác định của hàm số w=3x+2ln(x−2y) là:

Select one:
a. với mọi (x,y)
b. {(x,y):x−2y≥0}
c. {(x,y):x−2y≠0}
d. {(x,y):x−2y>0}
Phản hồi
Đúng. Đáp án đúng là: {(x,y):x−2y>0}. Vì: Biểu thức bên trong logarit phải lớn hơn 0. Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: {(x,y):x−2y>0}

Điểm (1, –2) thuộc miền xác định của hàm số:

Select one:
a. w=x+2y−−−−−√
b. w=ln(x2+y)
c. w=1−3x+2y2x+y
d. 1+3x+y−−−−−−−−√
Phản hồi
Đúng. Đáp án đúng là: √(1+3x+y) Vì: Thay x = 1, y = –2 vào các biểu thức chỉ biểu thức của đáp án D xác định giá trị Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: 1+3x+y−−−−−−−−√

Đạo hàm riêng theo biến x của hàm số w=(4x-3y)^2 là:
Select one:
a. w_x^’=2(4x-3y)
b. w_x^’=4(4x-3y)
c. w_x^’=8(4x-3y)
d. w_x^’=-6(4x-3y)
Phản hồi
Đúng. Đáp án đúng là: w_x^’=8(4x-3y) Vì: Lấy đạo hàm của hàm số theo biến x coi y là hằng số: w’_x=2.(4x-3y)×4=8(4x-3y)
Tham khảo: Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).

The correct answer is: w_x^’=8(4x-3y)

Hàm số w=x0,2y0,5 có đạo hàm riêng cấp 2 w′′xy là:

Select one:
a. 0,2x−0,8y0,5
b. 0,1×0,8y0,5
c. −0,1x−0,8y−0,5
d. $ 0,1x^{-0,8}y^{-0,5} $
Phản hồi
Đúng. Đáp án đúng là}}: $ 0,1x^{-0,8}y^{-0,5} $ {Vì:} $ w_{x}^{‘}=0,2x^{-0,8}y^{0,5} $ } Tiếp tục lấy đạo hàm theo y: {\fontsize{14pt}{16.8pt}\selectfont $ w”_{xy}= \left( w’_{x} \right) _{y}^{‘}=0,2.0,5x^{-0,8}y^{-0,5}=0,1x^{-0,8}y^{-0,5} $ } {Tham khảo:} }Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).}

The correct answer is: $ 0,1x^{-0,8}y^{-0,5} $

Miền xác định của hàm số $ w=\sqrt[]{1-x^{2}-2y^{2}} $ là:

Select one:
a. với mọi (x,y)
b. $ ( x,y):1-x^{2}-2y^{2} \neq 0 $
c. $( x,y) :1-x^{2}-2y^{2}=0 $
d. $( x,y) :1-x^{2}-2y^{2} \geq 0$
Phản hồi
Đáp án đúng là}}: $ \left\{ \left( x,y \right) :1-x^{2}-2y^{2} \geq 0 \right} $ {Vì:} }Biểu thức chứa căn bậc 2 có nghĩa khi biểu thức bên trong căn đó phải lớn hơn hoặc bằng 0. {Tham khảo:} }Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).}

The correct answer is: $( x,y) :1-x^{2}-2y^{2} \geq 0$

Cho hàm số y=2x−1−−−−−√3.(4−5x)2−−−−−−−√3 . Số điểm tới hạn của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
Vì: y′=6(3−5x)3(2x−1)2√3.4−5x√3 }} Ta thấy hàm số xác định với mọi x và y’ = 0 tại x = 3/5; y’ không xác định tại x = 1/2 và 4/5. ⇒ Hàm số có 3 điểm tới hạn. {Tham khảo: }}Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 3

Giả sử hàm sản xuất ngắn hạn của một doanh nghiệp là Q=30L2−−√3 . Giá trị sản phẩm hiện vật cận biên của lao động tại L = 27 là:

Select one:
a. 20/27
b. 90∛2
c. 270
d. 20/3
Phản hồi
Vì: Q′=30.23L√3=20L√3⇒Q′(27)=203 }} {Tham khảo: }}Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36).

The correct answer is: 20/3

Cho hàm lợi nhuận phụ thuộc vào mức sản lượng của một doanh nghiệp là: π=−Q3+15Q2+600Q+800 Lợi nhuận tối đa của doanh nghiệp là:

Select one:
a. 6800
b. 9800
c. 11800
d. 10800 Đúng
Phản hồi

The correct answer is: 10800

Cho hàm số y=2×3−3×2+9. Số điểm cực trị của hàm số là:

Select one:
a. 4
b. 3
c. 2 Đúng
d. 1
Phản hồi

The correct answer is: 2

Cho hàm số y=(2×2−5x+1).e−2x. Số điểm cực trị của hàm số là:

Select one:
a. 1
b. 2 Đúng
c. 3
d. 4
Phản hồi

The correct answer is: 2

Cho hàm số y=5−4x−−−−−√3 . Kết luận đúng về hàm số là:

Select one:
a. Hàm số không đạt cực đại. Đúng
b. Hàm số đạt giá trị cực đại tại x = 1
c. Hàm số đạt giá trị cực đại tại x = 2
d. Hàm số đạt giá trị cực đại tại x = 5/4
Phản hồi
Vì: y′=−43(5−4x)2√3<0 }} Do đó y không đạt cực trị {Tham khảo: }}Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: Hàm số không đạt cực đại.

Giả sử hàm sản xuất ngắn hạn của một doanh nghiệp là Q=2L−−√. Cho biết giá của một đơn vị sản phẩm là p = $5, giá thuê một đơn vị lao động là wL = $1. Mức sử dụng lao động cho lợi nhuận tối đa là:

Select one:
a. 25 Đúng
b. 36
c. 16
d. 49
Phản hồi

The correct answer is: 25

Một doanh nghiệp hoạt động trong thị trường cạnh tranh với giá bán một đơn vị sản phẩm là p = $40. Cho biết hàm chi phí của doanh nghiệp là: TC=3Q2+4Q+30 Mức sản lượng cho lợi nhuận tối đa là:

Select one:
a. 7
b. 6 Đúng
c. 5
d. 4
Phản hồi

The correct answer is: 6

Giá trị của hàm số w=3x+ey2x+y tại điểm (1, 0) là:

Select one:
a. 3/2
b. 2
c. 1
d. ½
Phản hồi
Đúng. Đáp án đúng là: 2 {Vì:} }Thay x = 1, y = 0 vào biểu thức ta tính được giá trị của hàm số: 3.1+e02.1+0=42=2 {Tham khảo:} }Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: 2

Đạo hàm riêng theo biến y của hàm số w=4×2+3xy−y3 tại điểm (1,2) là:

Select one:
a. 9
b. 14
c. –9
d. 10
Phản hồi
Đúng. Đáp án đúng là: –9 Vì: Lấy đạo hàm của hàm số theo biến y rồi thay x = 1, y = 2 vào tìm giá trị: w′y=3x−3y2; w′y(1,2)=3.1−3.22=−9. Tham khảo: Mục 4.4.1. Đạo hàm riêng tại một điểm (BG, tr. 51).

The correct answer is: –9

Giá trị của hàm số w=x3−2xy√x+2y tại điểm (1, 4) là:

Select one:
a. –1/2
b. –1/3
c. –1/9
d. 62/9
Phản hồi
{Vì:} }Thay x = 1, y = 4 vào biểu thức ta tính được giá trị của hàm số: 13−2.1.4√1+2.4=1−49=−13 {Tham khảo:} }Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).}

The correct answer is: –1/3

Đạo hàm riêng theo biến x của hàm số w=x3+xy2−3x+y là:

Select one:
a. y2+1
b. 3×2+y2−2
c. 3×2+y2−3
d. 3×2+y2
Phản hồi
{Đúng. Đáp án đúng là}}: 3×2+y2−3 {Vì:} }Lấy đạo hàm của hàm số theo biến x: w′x=(x3)′x+y2(x)′x−3(x)′x+0=3×2+y2−3 {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).

The correct answer is: 3×2+y2−3

Với hàm sản xuất dạng Cobb – Douglas Q=a.Kα Lβ(a, α, β>0) , theo quy luật lợi ích cận biên giảm dần các tham số α, β phải thỏa mãn điều kiện:

Select one:
a. α≤0,β≤0
b. α≥0,β≥0
c. α≥1,β≥1
d. α≤1,β≤1
Phản hồi
{Đúng. Đáp án đúng là}}: α≤1, β≤1 {Vì: Q′′KK=a.α.(α−1)Kα−2Lβ≤0; }} {\fontsize{14pt}{16.8pt}\selectfont Q′′LL=a.β(β−1)KαLβ−2 ≤0 } {Tham khảo: }}Mục 4.7.2. Đạo hàm riêng cấp 2 và quy luật lợi ích cận biên giảm dần (BG, tr. 55).}

The correct answer is: α≤1,β≤1

Xét hàm sản xuất Q =f(K, L) . Trong kinh tế học, giá trị f′K(K0, L0) được gọi là:

Select one:
a. giá trị sản phẩm hiện vật cận biên của lao động tại điểm (K_0,L_0).
b. giá trị cận biên của tư bản tại điểm (K_0,L_0).
c. giá trị sản phẩm hiện vật cận biên của tư bản tại điểm (K_0,L_0 ).
d. giá trị cận biên của lao động tại điểm (K_0,L_0).
Phản hồi
Đúng. Đáp án đúng là: giá trị sản phẩm hiện vật cận biên của tư bản tại điểm (K_0,L_0). Vì: Theo ý nghĩa kinh tế của đạo hàm riêng. Tham khảo: Mục 4.7.1. Đạo hàm riêng và giá trị cận biên (BG, tr. 54).

The correct answer is: giá trị sản phẩm hiện vật cận biên của tư bản tại điểm (K_0,L_0 ).

Giá trị của hàm số w=x2+2xy−3y2 tại điểm (1, –1) là:

Select one:
a. 6
b. 4
c. –4
d. 0
Phản hồi
Đúng. Đáp án đúng là: –4 Vì: Thay x = 1, y = –1 vào biểu thức ta tính được giá trị của hàm số: 12+2.1.(−1)−3.(−1)2=−4 Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: –4

Cho hàm số y=∛x. Số điểm tới hạn của hàm số là:
Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
Đúng. Đáp án đúng là: 1 Vì: y^’=1/(3∛(x^2 )) y’ không xác định tại x = 0 Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 1

Cho hàm(x2−3x+2).e−2x. Hàm số giảm trên:

Select one:
a. (2−12√,2+12√)
b. (2+12√,+∞)
c. (−∞,2−12√)∪(2+12√,+∞)
d. 2 khoảng (−∞,2−12√) và (2+12√,+∞)
Phản hồi
3TCg308

The correct answer is: (−∞,2−12√)∪(2+12√,+∞)

Cho hàm số y=(2x−3)1982 xác định trên [2,3]. Hàm số đạt giá trị nhỏ nhất tại:

Select one:
a. 3
b. 5/2
c. 2
d. 3/2
Phản hồi
Vì: y′=1982.(2x−3)1981.2 }} Giải y’ = 0 ta được nghiệm x = 3/2. Tính y(2), y(3) và y(3/2) để tìm GTNN {Tham khảo: }}Mục 3.2.5. Bài toán cực trị toàn thể (BG, tr.36).

The correct answer is: 2

Cho hàm số y=x2.lnx Số điểm tới hạn của hàm số là:

Select one:
a. 1 Đúng
b. 2
c. 3
d. 4
Phản hồi

The correct answer is: 1

Cho hàm số y=e−2×3+5×2−4x+1 . Số điểm cực trị của hàm số là:

Select one:
a. 1
b. 2 Đúng
c. 3
d. 4
Phản hồi

The correct answer is: 2

Cho hàm số y=3×2+e−x2+3. Số điểm tới hạn của hàm số là:

Select one:
a. 1
b. 2 Đúng
c. 3
d. 4
Phản hồi

The correct answer is: 3

Cho hàm số y=x3−4×2+5x−2 . Giá trị nhỏ nhất của hàm số trên [0,2] là:

Select one:
a. -3
b. -2 Đúng
c. 0
d. 1
Phản hồi

The correct answer is: -2

Cho hàm số y=x33−32×2+2x−1. Hàm số tăng trên:

Select one:
a. (-∞,1)∪(2,+∞)
b. (1,2)
c. (2,+∞)
d. 2 khoảng (-∞,1) và (2,+∞) Đúng
Phản hồi
a

The correct answer is: 2 khoảng (-∞,1) và (2,+∞)

Hàm số w=f(x, y) có đạo hàm riêng theo biến x w′x=3x−4y. Đạo hàm riêng cấp 2 w′′xy của hàm số là:

Select one:
a. w′′xy=3
b. w′′xy=4
c. w′′xy=−3
d. w′′xy=−4
Phản hồi
Đúng. Đáp án đúng là: w_xy^”=-4 Vì: Lấy đạo hàm riêng theo biến y của w_x^’ khi đó ta coi x là hằng số: w”_xy=(w’_x )_y^’=(3x-4y)_y^’=-4 Tham khảo: Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).

The correct answer is: w′′xy=−4

Hàm số 2 biến số w=f(x,y) có số đạo hàm riêng cấp 2 nhiều nhất là:

Select one:
a. 2
b. 4
c. 6
d. 8
Phản hồi
{Đúng. Đáp án đúng là}}: 4 {Vì:} }Hàm số 2 biến số {có thể có} 4 đạo hàm riêng cấp 2 là w”xx, w”xy, w”yx, w”yy {Tham khảo:} }Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).

The correct answer is: 4

Đạo hàm riêng theo biến x của hàm số w=x4+2x2y−3sinx+y√ là:

Select one:
a. w′x=4×3+4xy−cosx
b. w′x=4×3+4xy+3cosx
c. w′x=4×3+4xy−3cosx
d. w′x=2×2+12y√
Phản hồi
{Đúng. Đáp án đúng là}}: 4×3+4xy−3cosx. {Vì:} }Lấy đạo hàm của hàm số theo biến x. {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52). }

The correct answer is: w′x=4×3+4xy−3cosx

Biểu thức vi phân toàn phần của hàm số w=sin⁡(3x-2y) là:

Select one:
a. dw=3.cos(3x−2y)dx+2.cos(3x−2y) dy
b. dw=3.cos(3x−2y)dx−2cos(3x−2y) dy
c. dw=cos(3x−2y)dx+cos(3x−2y)dy
d. dw=3sin(3x−2y)dx−2sin(3x−2y)dy
Phản hồi
Đúng. Đáp án đúng là: dw=3.cos(3x−2y)dx−2cos(3x−2y) {Vì:} w′x=3cos(3x−2y),w′y=−2cos(3x−2y) } Lập theo công thức của biểu thức vi phân. Tham khảo: Mục 4.5. Vi phân (BG, tr. 52).}

The correct answer is: dw=3.cos(3x−2y)dx−2cos(3x−2y) dy

Đạo hàm riêng theo biến x của hàm số w=y2+yx+x−−√ là:

Select one:
a. w′x=yx2+12x√
b. w′x=−yx2+12x√
c. w′x=4×3+4xy−3cosx
d. w′x=2×2+12y√
Phản hồi
{Đúng. Đáp án đúng là}}: w′x=−yx2+12x√ {Vì:} }Lấy đạo hàm của hàm số theo biến x coi y là hằng số. Chú ý: (1x)′x=−1x2và(x−−√)′=12x√ {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).}

The correct answer is: w′x=−yx2+12x√

Đạo hàm riêng theo biến y của hàm số w=x4+x2y−sinx+2y√ là:

Select one:
a. 4×3+2xy−cosx
b. 4×3+x2+2y√
c. x2+2y√
d. x2+1y√
Phản hồi
{Đúng. Đáp án đúng là}}: x2+1y√ {Vì:} }Lấy đạo hàm của hàm số theo biến y. Coi x là hằng số. Chú ý: (y√)′y=12y√ {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).}

The correct answer is: x2+1y√

Hàm số w=(3x−2y)2 có tổng hai đạo hàm riêng cấp 2 w′′xy+w′′xx bằng:

Select one:
a. 6(3x – 2y)
b. 18
c. 6
d. 2(3x-2y)
Phản hồi
{Đúng. Đáp án đúng là}}: 6 {Vì:} w′x=6(3x−2y)=18x−12y } w′′xx = 18, w′′xy = –12 {Tham khảo: }}Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).}

The correct answer is: 6

Cho hàm số y=−4×2+7x−3−−−−−−−−−−−−√ . Giá trị lớn nhất của hàm số là:

Select one:
a. 0
b. 1
c. 1/2
d. 1/4 Đúng
Phản hồi

The correct answer is: 1/4

Cho hàm số y=(3x−1)x−−√. Hàm số tăng trên:

Select one:
a. (-∞,1/9)
b. (-∞,1/3)
c. (1/3,+∞)
d. (1/9,+∞) Đúng
Phản hồi

The correct answer is: (1/9,+∞)

Cho hàm số y=(5x−3)2.(4−7x)3 . Số điểm dừng nhưng \textbf{\textit{không}} phải là điểm cực trị của hàm số là:

Select one:
a. 1 Đúng
b. 2
c. 3
d. 4
Phản hồi

The correct answer is: 1

Giả sử doanh nghiệp độc quyền sản xuất một loại sản phẩm với hàm cầu là p=300-2Q. Doanh thu cận biên tại mức sản lượng Q = 9 là:

Select one:
a. 260
b. 282
c. 264 Đúng
d. 276
Phản hồi
Vì: TR=p.Q=(300−2Q)Q=−2Q2+300Q ⇒TR′=−4Q+300⇒TR′(9)=264 }} {Tham khảo: }}Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36)

The correct answer is: 264

Cho hàm số y=e−4×2+3x+1x−1 . Số điểm tới hạn của hàm số là:

Select one:
a. 0 Đúng
b. 1
c. 2
d. 3
Phản hồi

The correct answer is: 0

Cho hàm số y=esinx−sinx . Số điểm dừng của hàm số trên [−π2,π] là:

Select one:
a. 1
b. 2
c. 3
d. 4 Đúng
Phản hồi

The correct answer is: 4

Cho hàm số y=(x2−5x+4)10. Hàm số tăng trên:

Select one:
a. (−∞,1) và (4,+∞)
b. (1,52) và (4,+∞) Đúng
c. (−∞,1) và (52,4)
d. (1,4)
Phản hồi

The correct answer is: (1,52) và (4,+∞)

Giả sử doanh thu và chi phí của một nhà sản xuất được cho tương ứng bởi: TR=−70Q2+5000QTC=2Q3+20Q2−1000Q+4000 Lợi nhuận tối đa của doanh nghiệp là:

Select one:
a. 64.000 Đúng
b. 30.000
c. 32.000
d. 40.000
Phản hồi

The correct answer is: 64.000

Đạo hàm riêng theo biến y của hàm số w=x23x−2y là:

Select one:
a. w′y=2x(3x−2y)−3×2(3x−2y)2
b. w′y=−2x2y(3x−2y)2
c. w′y=2×2(3x−2y)2 Đúng
d. w′y=2x23x−2y
Phản hồi
{Đúng. Đáp án đúng là}}: w′y=2×2(3x−2y)2 {Vì:} }Lấy đạo hàm của hàm số theo biến y coi biến số x là hằng số: w′y=−x2(3x−2y)′y(3x−2y)2=2x2y(3x−2y)2 {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).}

The correct answer is: w′y=2×2(3x−2y)2

Đạo hàm riêng theo biến y của hàm số w=x2.y−x−−√.ey là:

Select one:
a. 2xy+ey2x√
b. x2y−x−−√.ey
c. x2−ey
d. $ x^{2}-\sqrt[]{x}.e^{y} $ Đúng
Phản hồi
Đúng. Đáp án đúng là: x^2-√x.e^y Vì:Lấy đạo hàm của hàm số theo biến y: $ w’_{y}=x^{2}. \left( y \right) ^{‘}_{y}-\sqrt[]{x}. \left( e^{y} \right) _{y}^{‘}=x^{2}.1-\sqrt[]{x}.e^{y} $ $ =x^{2}-\sqrt[]{x}.e^{y} $ {Tham khảo:} }Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52)

The correct answer is: $ x^{2}-\sqrt[]{x}.e^{y} $

Đạo hàm riêng theo biến x của hàm số w=ln⁡(4x-3y) tại điểm (1, 0) là:

Select one:
a. 1/4
b. 0
c. –3/4
d. 1 Đúng
Phản hồi
Đúng. Đáp án đúng là: 1 Vì: Lấy đạo hàm của hàm số theo biến x rồi\textbf{ }thay x = 1, y = 0 vào tìm giá trị của biểu thức: $ w’_{x}=\frac{4}{4x-3y}w’_{x} \left( 1,0 \right) =\frac{4}{4-0}=1 $ {Tham khảo:} }Mục 4.4.1. Đạo hàm riêng tại một điểm (BG, tr. 51)

The correct answer is: 1

Giá trị của hàm số w=ln(2x−y)+x3−2y tại điểm (1, 1) là:

Select one:
a. –2
b. ln⁡2-1
c. –1 Đúng
d. 1
Phản hồi
Đúng. Đáp án đúng là: –1 {Vì: }Thay x = 1, y = 1 vào biểu thức ta tính được giá trị của hàm số: ln(2.1−1)+13−2.1=ln1+1−2=−1 {Tham khảo:} }Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).}

The correct answer is: –1

Đạo hàm riêng theo biến $x$ của hàm số $w = 3x^2-2xy+y^3$ tại điểm $(1, 2)$ là:

Select one:
a. 14
b. 6
c. 2 Đúng
d. 10
Phản hồi
Đúng. Đáp án đúng là: 2 Vì: Lấy đạo hàm của hàm số theo biến x rồi thay x = 1, y = 2 vào tìm giá trị:

$w’_x=6x-2y$; $w’_x(1,2)=6.1-2.2=2$. Tham khảo: Mục 4.4.1. Đạo hàm riêng tại một điểm (BG, tr. 51).

The correct answer is: 2

Đường mức của hàm số w=x^2+3y^2-x ứng với mức w0 = 1 có phương trình là:
Select one:
a. x^2+3y^2-x=0
b. x^2+3y^2-x=1 Đúng
c. x^2+3y^2-x=-1
d. x^2+3y^2-x=2
Phản hồi
Đúng. Đáp án đúng là: x^2+3y^2-x=1 Vì: Cho w = w0 Tham khảo: Mục 4.1.5. Đường mức (BG, tr. 48).

The correct answer is: x^2+3y^2-x=1

Theo quy luật lợi ích cận biên giảm dần, hàm sản xuất Q=f(K,L) sẽ phải thỏa mãn điều kiện:

Select one:
a. Q′′KK≤0;Q′′KL≤0, ∀K,L>0
b. Q′′LK≤0;Q′′KL≤0, ∀K,L>0
c. Q′′KK≤0;Q′′LL≥0, ∀K,L>0
d. Q′′KK≤0;Q′′LL≤0, ∀K,L>0 Đúng
Phản hồi
{Đúng. Đáp án đúng là}}: Q′′KK≤0;Q′′LL≤0, ∀K,L>0 {Vì: }}Theo quy luật lợi ích cận biên giảm dần các đạo hàm riêng cấp 2 theo cùng 1 biến số phải âm. {Tham khảo: }}Mục 4.7.2. Đạo hàm riêng cấp 2 và quy luật lợi ích cận biên giảm dần (BG, tr. 55). }

The correct answer is: Q′′KK≤0;Q′′LL≤0, ∀K,L>0

Cho hàm số y=ln(2×2−4x+7) . Số điểm tới hạn của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
Vì: y′=4x−42×2−4x+7 }} Giải y’ = 0 suy ra 1 điểm tới hạn x = 1 {Tham khảo: }}Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).}

The correct answer is: 1

Cho hàm số y=x3−2×2+x+3 . Số điểm dừng của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi
Vì: y′=3×2−4x+1 Giải y′=0 ta được 2 nghiệm: y′=3×2−4x+1=0⇔x1=1;x2=13 ⇒x1=1;x2=13 là các điểm dừng. {Tham khảo:}} Mục 3.2.2. Điều kiện cần của cực trị (BG, tr.34).

The correct answer is: 2

Cho hàm số y=x4−8×3+22×2−24x+9 . Số điểm cực đại của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi

The correct answer is: 1

Giả sử hàm chi phí của một doanh nghiệp là TC=Q3−3Q+1 . Chi phí cận biên tại mức sản lượng Q = 3 là:

Select one:
a. 19
b. 25
c. 20
d. 24
Phản hồi
Đúng. Đáp án đúng là: 24 Vì: TC’=3Q^2-3 ⇒ TC’ (3)=24 Tham khảo: Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36).

The correct answer is: 24

Cho hàm số y=13×3−2×2+4x+3 . Số điểm cực trị của hàm số là:

Select one:
a. 0
b. 1
c. 2
d. 3
Phản hồi
Vì: y′=x2−4x+4=(x−2)2 }} Giải y’ = 0 ta được 1 nghiệm y′=0⇔x2−4x+4=0⇔x=2 y′≥0,∀x. ⇒ Hàm số không có cực trị. {Tham khảo: }}Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 0

Cho hàm số y=x.4−3x−−−−−√ . Giá trị lớn nhất của hàm số trên [−1,43] là:

Select one:
a. 0
b. 16/(9√3)
c. 20/(9√3)
d. 22/(9√3)
Phản hồi

The correct answer is: 16/(9√3)

Cho hàm số y=(5x−3)2.(4−7x)3 . Số điểm dừng nhưng \textbf{\textit{không}} phải là điểm cực trị của hàm số là:

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi

The correct answer is: 1

Vi phân của hàm số w=3×2+xy−y2 tại điểm x0=0,y0=1 ứng với Δx=0,01;Δy=0,02 bằng:

Select one:
a. 0,05
b. 0,03
c. −0,03
d. 0,0002
Phản hồi
{Đúng. Đáp án đúng là}}: −0,03 {Vì:} w′x=6x+y,w′y=x−2y } Tính theo công thức vi phân tại một điểm: {\fontsize{14pt}{16.8pt}\selectfont dw(0,1)=w′x(0,1).Δx+w′y(0,1).Δy=1.0,01+(−2).0,02=−0,03 } {Tham khảo:} }Mục 4.5. Vi phân (BG, tr. 52).}

The correct answer is: −0,03

Miền xác định của hàm số w=2x.sin3y−eyx−y là:

Select one:
a. [(x,y):x-y=0] b. [(x,y):x-y≠0] c. [(x,y):x-y>0] d. [(x,y):x-y<0] Phản hồi
Đúng. Đáp án đúng là: {(x,y):x-y≠0

The correct answer is: [(x,y):x-y≠0]

Điểm (2, –1) thuộc miền xác định của hàm số:

Select one:
a. w=ln(y2−x)
b. w=exy
c. w=y+2xx+2y
d. 1−3x−y−−−−−−−−√
Phản hồi
Đúng. Đáp án đúng là: w=e^xy Vì: Thay x = 2, y = –1 vào các biểu thức chỉ biểu thức của đáp án B xác định giá trị Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: w=exy

Miền xác định của hàm số w=x2+2xy−5y3+x−3y là:

Select one:
a. với mọi (x,y)
b. {(x,y):x>0,y>0}
c. {(x,y):x≠0,y≠0}
d. {(x,y):x2+2xy−5y3≠0}
Phản hồi
Đúng. Đáp án đúng là: với mọi (x,y) Vì: Biểu thức luôn có nghĩa với mọi giá trị của x và y. Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: với mọi (x,y)

Đường mức của hàm số w = 2x – 3y – 1 ứng với mức w0 = 2 có phương trình là:
Select one:
a. 2x-3y=2
b. 2x-3y=3
c. 2x-3y=1
d. 2x-3y=0
Phản hồi
Đúng. Đáp án đúng là: 2x-3y=3 Vì: Cho w = w0 và chuyển 1 sang vế phải: 2x – 3y – 1 = 2⇔2x –3y=3 Tham khảo: Mục 4.1.5. Đường mức (BG, tr. 48).

The correct answer is: 2x-3y=3

Hàm số w=f(x, y) có đạo hàm riêng theo biến x w′x=3x−4y. Đạo hàm riêng cấp 2 w′′xy của hàm số là:

The correct answer is: w′′xy=−4

Xét bài toán tìm cực trị của hàm số w=2x+3y với điều kiện ràng buộc là phương trình x2+3y2=28 . Hàm Lagrange L=2x+3y+λ(28−x2−3y2) có các đạo hàm riêng cấp 1 L′x=2−2λx;L′y=3−6λy. Hàm số L có điểm dừng là M0(x0,y0,λ0) với y0=−2 và λ0 có giá trị là:

Select one:
a. 1
b. 2
c. -1/4
d. 1/2
Phản hồi
{Đúng. Đáp án đúng là: −14 }} {Vì: }}Thay y=−2 vào phương trình L′y=0 tìm được giá trị của λ0 . Ta có: 3−6.λ.(−2)=0⇒λ=−14 {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: -1/4

Sử dụng phương pháp nhân tử Lagrange giải bài toán tìm cực trị có điều kiện, ta biết rằng hàm Lagrange L có điểm dừng M0(x0,y0,−12) và L′′xx=−2λ;L′′xy=L′′yx=0;L′′yy=−4λ;g′x=3;g′y=1 . Khi đó tại điểm (x0,y0), hàm số với điều kiện đã cho:

Select one:
a. đạt giá trị cực đại.
b. đạt giá trị cực tiểu.
c. không đạt cực trị.
d. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của x_0,y_0.
Phản hồi

The correct answer is: đạt giá trị cực tiểu.

3TCc511

Select one:
a. D<0
b. D>0;a_11>0
c. D>0;a_11<0
d. D=0
Phản hồi
Đúng. Đáp án đúng là: D>0;a_11

The correct answer is: D>0;a_11<0

Hàm số 2 biến số w = f(x, y) có các đạo hàm riêng w′x, w′y . Điểm M0(x0,y0 ) mà tại đó các đạo hàm riêng cấp 1 triệt tiêu:

w′x=0w′y=0

được gọi là:

Select one:
a. điểm triệt tiêu của hàm số.
b. điểm dừng chân của hàm số.
c. điểm dừng của hàm số.
d. điểm nghi ngờ của hàm số.
Phản hồi
Đúng. Đáp án đúng là: điểm dừng của hàm số. Vì: Điểm các đạo riêng cấp 1 của hàm số triệt tiêu được gọi là điểm dừng của hàm số. Tham khảo: Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).

The correct answer is: điểm dừng của hàm số.

Hàm số w=3×2+y2−3x−2y có điểm dừng là:

Select one:
a. M0(12;1)
b. M0(1;1)
c. M0(2;1)
d. M0(−12;1)
Phản hồi

The correct answer is: M0(12;1)

Hàm số w=f(x, y) có các đạo hàm riêng là w′x=2mx+y−3;w′y=x−5 trong đó m là tham số. Điểm M0(5,−1) là điểm dừng của hàm số w khi m có giá trị là:

Select one:
a. 5/2
b. 5
c. 2/5
d. −5
Phản hồi
{Đúng. Đáp án đúng là: 2/5 }} {Vì: }}Thay x=5,y=−1 , tìm m để 2 đạo hàm riêng đều triệt tiêu. 2.5.m+(−1)−3=05−5=0⇔m=25 {Tham khảo: }}Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).}

The correct answer is: 2/5

Xét hàm số 2 biến số w=f(x,y) có các đạo hàm riêng: w′x=3×2−2y−1;w′y=−2x+2y . Biết rằng điểm M0(−13,−13) là điểm dừng của hàm số, khi đó điểm dừng M0 :

Select one:
a. là điểm cực đại của hàm số.
b. là điểm cực tiểu của hàm số.
c. không là điểm cực trị của hàm số.
d. có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Phản hồi

The correct answer is: không là điểm cực trị của hàm số.

Tính tích phân: ∫3x+22×2+x−3⋅dx

Select one:
a. ln|x−1|+2ln|2x+3|+C
b. ln|x−1|−2ln|2x+3|+C
c. −ln|x−1|+ln|2x+3|+C
d. ln|x−1|+12ln|2x+3|+C
Phản hồi

The correct answer is: ln|x−1|+12ln|2x+3|+C

Tính tích phân: ∫sin3x⋅dx

Select one:
a. cos2x2−cosx+C
b. cos3x3−cosx+C
c. cos2x2+cosx+C
d. cos3x3+cosx+C
Phản hồi
{Đúng. Đáp án đúng là: cos3x3−cosx+C }} {Vì: }}Sử dụng tính bất biến của tích phân để ra kết quả ∫sin3x⋅dx=−∫sin2x.d(cosx)=∫(cos2x−1)d(cosx)=cos3x3−cosx+C {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)}

The correct answer is: cos3x3−cosx+C

Tính tích phân: I=∫(x2−2x+4x).dx

Select one:
a. x33+x2−4ln|x|+C
b. x33−x2+4ln|x|+C
c. 2x−2−4×2+C
d. 2x+2+4×2+C
Phản hồi
{Đúng. Đáp án đúng là: x33−x2+4ln|x|+C }} {Vì: }}Khai triển tích phân và áp dụng các công thức tích phân cơ bản ta được kết quả I=∫(x2−2x+4x).dx=∫x2.dx−2.∫x.dx+4.∫dxx=x33−x2+4ln|x|+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)}

The correct answer is: x33−x2+4ln|x|+C

Tính tích phân: ∫(x2+1)3⋅dx

Select one:
a. x77+3⋅x55+x3+x+C
b. x77−3⋅x55+x3−x+C
c. −x77+3⋅x55−x3+x+C
d. x77+3⋅x55+x3+C
Phản hồi
Đúng. Đáp án đúng là: x77+3⋅x55+x3+x+C }} {Vì: }}Sử dụng công thức tích phân cơ bản ∫(x2+1)3⋅dx=∫(x6+3×4+3×2+1)dx =x77+3⋅x55+x3+x+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: x77+3⋅x55+x3+x+C

Tính tích phân:

I=∫dx1+x+1−−−−√3

3TCp632

Select one:
a. a
b. b
c. c
d. d
Phản hồi

The correct answer is: b

Tính tích phân: ∫x⋅(x2+1)9⋅dx

Select one:
a. 110⋅(x2+1)10+C
b. −110⋅(x2+1)10+C
c. 120⋅(x2+1)10+C
d. −120⋅(x2+1)10+C
Phản hồi

The correct answer is: 120⋅(x2+1)10+C

Tính tích phân: ∫sin3x⋅cos2x⋅dx

Select one:
a. cos5x5−cos3x3+C
b. cos5x5+cos3x3+C
c. sin5x5−sin3x3+C
d. sin5x5+sin3x3+C
Phản hồi

The correct answer is: cos5x5−cos3x3+C

Kết quả đúng của tích phân: I=∫2x.32xdx

Select one:
a. 2xln2⋅9xln9+C
b. 18xln18+C
c. −18xln18+C
d. 6xln6+C
Phản hồi
Đúng. Đáp án đúng là: 18xln18+C }} {Vì: I=∫2x.32xdx=∫18x.dx=18xln18+C }} {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)}

The correct answer is: 18xln18+C

Hàm số 2 biến số w=f(x, y) có đạo hàm riêng theo biến x là w′y=2x+y−3 . Biết rằng hàm số w có điểm dừng là M0(x0,y0) với x0=3/2 , khi đó giá trị y0 là:

Select one:
a. ½
b. 2/3
c. 3
d. 0
Phản hồi
{Đúng. Đáp án đúng là: }}0 {Vì: }}Điểm dừng thỏa mãn w′y=0 , thay x = 3/2 vào, giải tìm được giá trị của y: 2.32+ y – 3 =0=> y = 0 {Tham khảo: }}Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).}

The correct answer is: 0

Khi giải bài toán tìm cực trị của hàm số w=x.y với điều kiện ràng buộc là phương trình 3x+y=12 , hàm Lagrange có các đạo hàm riêng cấp 1 là L′x=y−3λ;L′y=x−λ Khi đó, điểm dừng của hàm Lagrange L là M0(x0,y0,λ0) với:

Select one:
a. x0=−2;y0=6;λ0=2
b. x0=2;y0=−6;λ0=−2
c. x0=2;y0=6;λ0=2
d. x0=−2;y0=6;λ0=−2
Phản hồi

The correct answer is: x0=2;y0=6;λ0=2

Sử dụng phương pháp nhân tử Lagrange giải bài toán tìm cực trị có điều kiện, ta biết rằng hàm Lagrange L có điểm dừng M0(x0,y0,12) và L′′xx=−2λ;L′′xy=L′′yx=0;L′′yy=−4λ;g′x=3;g′y=−1 . Khi đó tại điểm (x0,y0), hàm số với điều kiện đã cho:

The correct answer is: đạt giá trị cực đại.

Hàm số 2 biến số w=f(x, y) có đạo hàm riêng theo biến x là w′x=3x−2y+1 Biết rằng hàm số w có điểm dừng là M0(x0,y0) với x0=2 , khi đó giá trị y0 là:

Select one:
a. 7
b. 7/2
c. 2
d. 3
Phản hồi
Đúng. Đáp án đúng là: 7/2 Vì: Điểm dừng thỏa mãn w_x^’=0, thay x = 2 vào, giải tìm được giá trị của y: 3.2–2y+1= 0⇔2y=7⇔y=7/2Tham khảo: Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).

The correct answer is: 7/2

Hàm số 2 biến số w=f(x, y) có đạo hàm riêng theo biến x là w′x=x2−3xy+1 . Biết rằng hàm số w có điểm dừng là M0(x0,y0) với x0=1 , khi đó giá trị y0 là:

Select one:
a. –2/3
b. 2/3
c. 1
d. 0
Phản hồi
{Đúng. Đáp án đúng là: }}2/3 {Vì: }}Điểm dừng {thỏa mãn} w′x=0 , thay x = 1 vào, giải tìm được giá trị của y: 12−3.1.y+1=0⇔y=23 {Tham khảo: }}Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).}

The correct answer is: 2/3

Thực hiện giải bài toán cực trị có điều kiện ràng buộc bằng phương pháp nhân tử Lagrange. Tại điểm dừng M0(x0,y0,λ0) của hàm số Lagrange, xét điều kiện đủ, ta có ma trận

|H¯¯¯¯¯|=∣∣∣∣02−1201−110∣∣∣∣

Khi đó, ta kết luận được: tại điểm x0,y0) hàm số

Select one:
a. đạt giá trị cực đại.
b. đạt giá trị cực tiểu.
c. không đạt cực trị.
d. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của λ_0.
Phản hồi
{Đúng. Đáp án đúng là: }}đạt giá trị cực tiểu {Vì: }}Tính định thức cấp 3: |H¯¯¯¯¯|=0−2−2−(0+0+0)=−4<0 . {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: đạt giá trị cực tiểu.

Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3×2+y2=28 . Hàm Lagrange L=3x+2y+λ(28−3×2−y2) có các đạo hàm riêng cấp 1 L′x=3−6λx;L′y=2−2λy. Hàm số L có điểm dừng là M0(x0,y0,λ0) khi đó:

Select one:
a. x0=2y0
b. x0=−2y0
c. y0=2×0
d. y0=−2×0
Phản hồi
{Đúng. Đáp án đúng là: y0=2×0 }} {Vì: }}Từ 2 phương trình L′y=0,L′x=0 biểu diễn x, y qua λ từ đó rút được tỉ lệ giữa x và y. 3−6λx=0⇒x=12λ2−2λy=0⇒y=1λ⇒y=2x {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: y0=2×0

Tính tích phân: ∫cos2xcosx+sinx⋅dx

Select one:
a. −sinx+cosx+C
b. sinx−cosx+C
c. −sinx−cosx+C
d. sinx+cosx+C
Phản hồi
Đúng. Đáp án đúng là: sinx+cosx+C }} {Vì:}} { ∫cos2xcosx+sinx⋅dx=∫cos2x−sin2xcosx+sinx⋅dx =∫(cosx−sinx).dx=sinx+cosx+C }} {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: sinx+cosx+C

Tính tích phân: I=∫tan2x⋅dx

Select one:
a. tan2x−2x+C
b. tan2x+2x+C
c. tanx−x+C
d. tanx+x+C
Phản hồi
Đúng. Đáp án đúng là: tanx−x+C }} {Vì: }} I=∫tan2x⋅dx=∫(1cos2x−1)⋅dx=tanx−x+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: tanx−x+C

3TCc622.PNG

Select one:
a. 23⋅(1+lnx)32+C
b. 23⋅(1+lnx)23+C
c. (1+lnx)32+C
d. (1+lnx)23+C
Phản hồi

The correct answer is: 23⋅(1+lnx)32+C

3TCc620.PNG

Select one:
a. 1x+1+ln|x+1|+C
b. 2x+1+ln|x+1|+C
c. 4x+1+ln|x+1|+C
d. 4x+1−ln|x+1|+C
Phản hồi

The correct answer is: 4x+1+ln|x+1|+C

Kết quả đúng của tích phân: I=∫(x2+x+1).lnx.dx

Select one:
a. (x33+x22+x)⋅lnx−(x39+x24+x)+C
b. (x33−x22+x)⋅lnx+(x39+x24+x)+C
c. (x33−x22−x)⋅lnx+(x39+x24+x)+C
d. (x33+x22+x)⋅lnx+(x39+x24+x)+C
Phản hồi

The correct answer is: (x33+x22+x)⋅lnx−(x39+x24+x)+C

Tính tích phân: I=∫e8x.dx

Select one:
a. 18e8x+C
b. 8e8x+C
c. e8x+C
d. – e8x+C
Phản hồi
Đúng. Đáp án đúng là: 18e8x+C }} {Vì: I=∫e8x.dx=18∫e8x.d(8x)=18e8x+C }} {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)}

The correct answer is: 18e8x+C

Tinh tích phân: ∫x+1×2−7x+10⋅dx

Select one:
a. 2ln|x−5|−ln|x−2|+C
b. 3ln|x−5|−2ln|x−2|+C
c. −3ln|x−5|+2ln|x−2|+C
d. −2ln|x−5|+ln|x−2|+C
Phản hồi
Đúng. Đáp án đúng là: 2ln|x−5|−ln|x−2|+C }} {Vì: }}Sử dụng công thức tích phân cơ bản ∫x+1×2−7x+10⋅dx=∫(2x−5−1x−2).dx=2ln|x−5|−ln|x−2|+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: 2ln|x−5|−ln|x−2|+C

Tính tích phân: ∫lnx⋅dx

Select one:
a. x(lnx−1)+C
b. x(lnx+1)+C
c. x2(lnx+1)+C
d. −x2(lnx+1)+C
Phản hồi
Đúng. Đáp án đúng là: x(lnx−1)+C }} {Vì: ∫lnx⋅dx=xlnx−∫dx=xlnx−x+C }} {Tham khảo: }}Mục 6.4.4. Phương pháp tích phân từng phần (BG, tr.79)

The correct answer is: x(lnx−1)+C

Xét bài toán tìm cực trị của hàm số w=x.y với điều kiện 3x−y=5 . Khi sử dụng phương pháp nhân tử Lagrange, hàm Lagrange là:

Select one:
a. L=x.y+λ(5−3x−y)
b. L=x.y+λ(5−3x+y)
c. L=3x−y+λ(5−x.y)
d. L=5−3x+y−λx.y
Phản hồi
{Đúng. Đáp án đúng là: L=x.y+λ(5−3x+y) }} {Vì: }}Hàm x.y là hàm Mục tiêu, phương trình ràng buộc là 3x−y=5 . {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: L=x.y+λ(5−3x+y)

3TCc514.PNG

Select one:
a. là điểm cực đại của hàm số.
b. là điểm cực tiểu của hàm số.
c. không là điểm cực trị của hàm số.
d. là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a_11.
Phản hồi
Đúng. Đáp án đúng là: là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a_11 Vì: Theo điều kiện đủ của cực trị. Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị (BG, tr.60).

The correct answer is: là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a_11.

3TCc528.PNG

Select one:
a. đạt giá trị cực đại.
b. đạt giá trị cực tiểu.
c. không đạt cực trị.
d. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của λ_0.
Phản hồi
{Đúng. Đáp án đúng là: }}đạt giá trị cực đại. {Vì: }}Tính định thức cấp 3: |H¯¯¯¯¯|=0+2+2−(0+0+0)=4>0 . {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: đạt giá trị cực đại.

Select one:
a. x_0=4;y_0=2
b. x_0=-4;y_0=-2
c. x_0=2;y_0=4
d. x_0=-2;y_0=-4
Phản hồi
{Đúng. Đáp án đúng là: x0=−2;y0=−4 }} {Vì: }}Thay λ=−14 vào phương trình L′y=0 tìm y, thay vào phương trình L′x=0 tìm x. Ta có: 3−6.(−14)x=0⇒x=−22−2.(−14)y=0⇒y=−4 {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: x_0=-2;y_0=-4

3TCc513.PNG

Select one:
a. là điểm cực đại của hàm số.
b. là điểm cực tiểu của hàm số.
c. không là điểm cực trị của hàm số.
d. là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a_11.
Phản hồi
Đúng. Đáp án đúng là: không là điểm cực trị của hàm số.Vì: Theo điều kiện đủ của cực trị. Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị (BG, tr.60).

The correct answer is: không là điểm cực trị của hàm số.

Điểm cực đại và điểm cực tiểu của hàm số được gọi chung là:

Select one:
a. điểm tối ưu.
b. điểm tốt nhất.
c. điểm cực trị.
d. điểm tìm được.
Phản hồi
Đúng. Đáp án đúng là: điểm cực trị. Vì: Theo tên gọi. Tham khảo: Mục 5.1.1. Khái niệm cực trị (BG, tr.60).

The correct answer is: điểm cực trị.

Xét bài toán tìm cực trị của hàm số w=2x−3y với điều kiện ràng buộc là phương trình x2+3y2=28 . Hàm Lagrange L=2x−3y+λ(28−x2−3y2) có các đạo hàm riêng cấp 1 L′x=2−2λx;L′y=−3−6λy. Hàm số L có điểm dừng là M0(x0,y0,λ0) với x0=2 và λ0 có giá trị là:

Select one:
a. 1
b. 2
c. –1/2
d. 1/2
Phản hồi
{Đúng. Đáp án đúng là: 12 }} {Vì: }}Thay x = 2 vào phương trình L′x=0 tìm được giá trị của λ0 . Ta có: 2−2.λ.2=0⇒λ=12 {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: –1/2

Tính tích phân: I=∫dx3sinx+4cosx+5

Select one:
a. 23+tanx2+C
b. −23+tanx2+C
c. 23+tanx+C
d. −23+tanx+C
Phản hồi

The correct answer is: −23+tanx2+C

Tính tích phân: I=∫2sin2x2⋅dx

Select one:
a. x+sin⁡x+C
b. x-sin⁡x+C
c. x+cosx+C
d. x-cosx+C
Phản hồi
Đúng. Đáp án đúng là: x−sinx+C }} {Vì: }}Sử dụng công thức lượng giác, sau đó áp dụng công thức tích phân cơ bản. I=∫2sin2x2⋅dx=∫(1−cosx).dx=x−sinx+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: x-sin⁡x+C

Tính tích phân: I=∫cotx⋅dx

Select one:
a. ln|cosx|+C
b. ln|cos2x|+C
c. ln|sinx|+C
d. ln|sin2x|+C
Phản hồi
Đúng. Đáp án đúng là: ln|sinx|+C }} {Vì:}} { I=∫cotx⋅dx=∫cosxdxsinx =∫d(sinx)sinx=ln|sinx|+C }} {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)

The correct answer is: ln|sinx|+C

Tính tích phân: ∫e3x−1ex−1⋅dx

Select one:
a. 12⋅e2x+ex+C
b. −12⋅e2x+ex+x+C
c. −12⋅e2x−ex+x+C
d. 12⋅e2x+ex+x+C
Phản hồi
Đúng. Đáp án đúng là: 12⋅e2x+ex+x+C }} {Vì: }}Sử dụng tính bất biến của tích phân để ra kết quả { ∫e3x−1ex−1⋅dx=∫(e2x+ex+1)dx =∫e2x.dx+∫ex.dx+∫dx=e2x2+ex+x+C }} {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: 12⋅e2x+ex+x+C

Tính tích phân: I=∫〖(x+sin⁡x )^2⋅dx〗

Select one:
a. a
b. b
c. c
d. d
Phản hồi

The correct answer is: c

Tính tích phân: I=∫x.e3x.dx

Select one:
a. 13x.e3x−19.e3x+C
b. 13x.e3x+19⋅e3x+C
c. 12x.e3x+19.e3x+C
d. 12x.e3x−19⋅e3x+C
Phản hồi

The correct answer is: 13x.e3x−19.e3x+C

Tính tích phân: ∫(3x+1)8⋅dx

Select one:
a. 127⋅(3x+1)9+C
b. −127⋅(3x+1)9+C
c. 24⋅(3x+1)7+C
d. −24⋅(3x+1)7+C
Phản hồi
Đúng. Đáp án đúng là: 127⋅(3x+1)9+C }} {Vì: }}Sử dụng tính bất biến của tích phân để ra kết quả ∫(3x+1)8⋅dx=13∫(3x+1)8⋅d(3x+1) =127⋅(3x+1)9+C {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)

The correct answer is: 127⋅(3x+1)9+C

Tính tích phân:I = ∫dxsinx

The correct answer is: ln|tanx2|+C

Xét hàm số 2 biến số w=f(x,y) có các đạo hàm riêng: w′x=−2x−2y−3;w′y=−2x−6y+1 . Biết rằng điểm M0(−52,1) là điểm dừng của hàm số, khi đó điểm dừng M0 :

The correct answer is: là điểm cực đại của hàm số.

Xét bài toán: Giả sử doanh nghiệp cạnh tranh thuần tuý sản xuất 2 loại sản phẩm với hàm chi phí kết hợp: TC=4Q21+2Q1Q2+3Q22+5. Với giá thị trường của sản phẩm 1 là $40 và giá của sản phẩm 2 là $35, hãy chọn một cơ cấu sản lượng (Q\textsubscript{1}, Q\textsubscript{2}) để hàm lợi nhuận đạt giá trị tối đa. Để giải bài toán thông qua việc tìm cực trị của hàm số, ta sẽ tìm cực đại của hàm lợi nhuận:

Select one:
a. π=35Q1+40Q2−(4Q21+2Q1Q2+3Q22+5)
b. π=35Q1+40Q2+(4Q21+2Q1Q2+3Q22+5)
c. π=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5)
d. π=40Q1+35Q2+(4Q21+2Q1Q2+3Q22+5)
Phản hồi
{Đúng. Đáp án đúng là: π=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5) }} {Vì: }}Doanh thu của doanh nghiệp là TR=40Q1+35Q2 =TR−TC=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5) {Tham khảo: }}Mục 5.2.1. Chọn mức sản lượng tối ưu (BG, tr.63).}

The correct answer is: π=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5)

Xét hàm số 2 biến số w=f(x,y). Ký hiệu: a11,a12,a21,a22 lần lượt là giá trị của các đạo hàm riêng cấp 2 w′′xx,w′′xy, w′′yx,w′′yy tính tại điểm dừng M0(x0,y0). Khi đó, định thức D để xét điều kiện đủ của cực trị là:

Select one:
a. D=∣∣∣a11a21a12a22∣∣∣
b. D=∣∣∣a11a12a22a21∣∣∣
c. D=∣∣∣a11a21a22a12∣∣∣
d. D=∣∣∣a11a21a12a11∣∣∣
Phản hồi

The correct answer is: D=∣∣∣a11a21a12a22∣∣∣

Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3×2+y2=7 . Sử dụng phương pháp nhân tử Lagrange với hàm Lagrange L=3x+2y+λ(7−3×2−y2) ta biết hàm số đạt giá trị cực đại tại điểm (x0=1;y0=2) ứng với λ0=12 . Nếu điều kiện ràng buộc được thay bằng phương trình 3×2+y2=8 thì giá trị cực đại của hàm số sẽ:

Select one:
a. tăng 1 đơn vị.
b. giảm 2 đơn vị.
c. giảm 1/2 đơn vị.
d. tăng 1/2 đơn vị
Phản hồi
{Đúng. Đáp án đúng là: }}tăng 12 đơn vị. {Vì: }}Theo ý nghĩa của nhân tử Lagrange: dw¯¯¯¯db=λ¯¯¯ {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: tăng 1/2 đơn vị

Xét bài toán: Giả sử người tiêu dùng có hàm lợi ích u=x0,4.y0,5. Trong điều kiện giá của hàng hóa thứ nhất là $4, giá của hàng hóa thứ hai là $5 và thu nhập dành cho tiêu dùng là $200 hãy xác định giỏ hàng đem lại lợi ích tối đa cho người tiêu dùng. Khi sử dụng phương pháp nhân tử Lagrange tìm cực đại của hàm lợi ích thì hàm Lagrange là:

Select one:
a. L=x0,4y0,5+λ(200−4x−5y)
b. L=x0,4y0,5+λ(200+4x+5y)
c. L=x0,4y0,5+λ(200−4x+5y)
d. L=x0,4y0,5+λ(200+4x−5y)
Phản hồi
{Đúng. Đáp án đúng là: L=x0,4y0,5+λ(200−4x−5y) }} {Vì: }}Điều kiện ràng buộc ngân sách là 4x+5y=200 . {Tham khảo: }}Mục 5.4. Ứng dụng trong kinh tế học: Bài toán tối đa hóa lợi ích tiêu dùng (BG, tr.66).}

The correct answer is: L=x0,4y0,5+λ(200−4x−5y)

Xét hàm số 2 biến số w=f(x,y) có các đạo hàm riêng: w′x=3×2−2y−1;w′y=−2x+2y . Biết rằng điểm M0(1,1) là điểm dừng của hàm số, khi đó điểm dừng M0 :

The correct answer is: là điểm cực tiểu của hàm số.

3TCc512

Select one:
a. D<0;a11<0
b. D>0;a11>0
c. D>0;a11<0
d. D<0;a11>0
Phản hồi
Đúng. Đáp án đúng là: D>0;a_11>0 Vì: Theo điều kiện đủ của cực trị. Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị (BG, tr.60).

The correct answer is: D>0;a11>0

Tính tích phân: I=∫dxcosx

The correct answer is: ln|tan(x2+π4)|+C

Tính tích phân:

I=∫cosx.cos2x.cos3x.dx.

Select one:
a. a
b. b
c. c
d. d
Phản hồi

The correct answer is: a

Tính tích phân: ∫3×2+2xx+1⋅dx

Select one:
a. 3×22+x−ln|x+1|+C
b. −3×22−x+ln|x+1|+C
c. 3×22−x+ln|x+1|+C
d. 3×22−x−ln|x+1|+C
Phản hồi
Đúng. Đáp án đúng là: 3×22−x+ln|x+1|+C }} {Vì: }}Sử dụng công thức tích phân cơ bản { ∫3×2+2xx+1⋅dx=∫(3x−1+1x+1)⋅dx=3×22−x+ln|x+1|+C }} {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)

The correct answer is: 3×22−x+ln|x+1|+C

Tính tích phân: I=∫cos4x.dx

Select one:
a. 38x+14sin2x+132sin4x+C
b. 38x−14sin2x+116sin4x+C
c. 38x−14sin2x−116sin4x+C
d. −38x+14sin2x+116sin4x+C
Phản hồi

The correct answer is: 38x+14sin2x+132sin4x+C

Tính tích phân}: ∫x2dxx3+1√

Select one:
a. x3+1−−−−−√+C
b. – x3+1−−−−−√+C
c. −23×3+1−−−−−√+C
d. 23×3+1−−−−−√+C
Phản hồi
Đúng. Đáp án đúng là: 23×3+1−−−−−√+C }} {Vì: ∫x2dxx3+1√=13∫d(x3+1)x3+1√=23×3+1−−−−−√+C }} {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)

The correct answer is: 23×3+1−−−−−√+C

Kết quả đúng của tích phân: I=∫1x⋅lnx⋅dx

Select one:
a. ln2x2+C
b. −ln2x2+C
c. x⋅lnx+C
d. −x⋅lnx+C
Phản hồi
{Đúng. Đáp án đúng là: ln2x2+C }} {Vì: }} I=∫1x⋅lnx⋅dx=∫lnx⋅d(lnx)=ln2x2+C {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74)}

The correct answer is: ln2x2+C

Tinh tích phân:

∫ex⋅dxex+1

Select one:
a. 2ln(ex+1)+C
b. −2ln(ex+1)+C
c. −ln(ex+1)+C
d. ln(ex+1)+C
Phản hồi
Đúng. Đáp án đúng là: ln(ex+1)+C }} {Vì:}} { ∫ex⋅dxex+1=∫d(ex+1)ex+1=ln(ex+1)+C }} {Tham khảo: }}Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74

The correct answer is: ln(ex+1)+C

Tính tích phân: I=∫x.lnx.dx

Select one:
a. −12x2lnx−14×2+C
b. 12x2lnx−14×2+C
c. x2lnx−12×2+C
d. x2lnx+12×2+C
Phản hồi

The correct answer is: 12x2lnx−14×2+C

Hàm số w=f(x, y) có các đạo hàm riêng là w′x=2x+my−3;w′y=mx−6y−5 trong đó m là tham số. Điểm M0(1,−1) là điểm dừng của hàm số w khi m có giá trị là:

Select one:
a. -1
b. 1
c. 0
d. ½
Phản hồi

The correct answer is: -1

Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3×2+y2=7 . Sử dụng phương pháp nhân tử Lagrange với hàm Lagrange L=3x+2y+λ(7−3×2−y2) ta biết hàm số đạt giá trị cực tiểu tại điểm (x0=−1;y0=−2) ứng với λ0=−12 . Nếu điều kiện ràng buộc được thay bằng phương trình 3×2+y2=8 thì giá trị cực đại của hàm số sẽ:

Select one:
a. tăng 1 đơn vị.
b. giảm 2 đơn vị.
c. giảm 1/2 đơn vị.
d. tăng 1/2 đơn vị.
Phản hồi
{Đúng. Đáp án đúng là: }}giảm 12 đơn vị. {Vì: }}Theo ý nghĩa của nhân tử Lagrange: dw¯¯¯¯db=λ¯¯¯ {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: giảm 1/2 đơn vị.

Xét hàm số 2 biến số w=f(x,y) có các đạo hàm riêng: w′x=2x−2y+1;w′y=−2x+4y+3 . Biết rằng điểm M0(−52,−2) là điểm dừng của hàm số, khi đó điểm dừng M0 :

The correct answer is: là điểm cực tiểu của hàm số.

Hàm số w=x2−y2+3x−2y có điểm dừng là:

Select one:
a. M0(32;1)
b. M0(3;−1)
c. M0(−32;12)
d. M0(−32;−1)
Phản hồi

The correct answer is: M0(−32;−1)

Hàm số w=x2+2xy−y2+3x có điểm dừng là:

Select one:
a. M0(−34;−34)
b. M0(34;34)
c. M0(−34;34)
d. M0(34;−34)
Phản hồi

The correct answer is: M0(−34;−34)

Khi giải bài toán tìm cực trị của hàm số w=x2+y2 với điều kiện ràng buộc là phương trình 3x+2y=26 , hàm Lagrange L có điểm dừng là M0(x0,y0,λ0) với y0=λ0=4 và x0 có giá trị là:

Select one:
a. 4
b. 2
c. 3/2
d. 6
Phản hồi
Đúng. Đáp án đúng là: 6 Vì: Thay y = 4 vào phương trình ràng buộc tìm x. Ta có: 3x + 2.4 = 26 → x = 6 Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: 6

Xét bài toán tìm cực trị của hàm số w=f(x,y) với điều kiện g(x,y)=b. Khi sử dụng phương pháp nhân tử Lagrange, hàm Lagrange là:

Select one:
a. L=λf(x,y)+[b−g(x,y)] b. L=f(x,y)+[b−λg(x,y)] c. L=f(x,y)+λ[b−g(x,y)] d. L=f(x,y)+[λb −g(x,y)] Phản hồi
{Đúng. Đáp án đúng là: L=f(x,y)+λ[b−g(x,y)] }} {Vì: }}{Cách} lập hàm Lagrange. {Tham khảo: }}Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).}

The correct answer is: L=f(x,y)+λ[b−g(x,y)]

Tính tích phân:

I=∫x.ex(x+1)2dx

p635.png

Select one:
a. a
b. b
c. c
d. d
Phản hồi

The correct answer is: c

Tính tích phân: ∫dx1−cos2x

Select one:
a. −cotx+C
b. cotx+C
c. −12cotx+C
d. 12cotx+C
Phản hồi
{Đúng. Đáp án đúng là: −12cotx+C }} {Vì: }}Áp dụng công thức tích phân cơ bản để ra kết quả ∫dx1−cos2x=∫dx2sin2x=−12⋅cotx+C {Tham khảo: }}Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73)}

The correct answer is: −12cotx+C

Tính tích phân: ∫ex⋅sinx⋅dx

Select one:
a. ex⋅(sinx+cosx)2+C
b. −ex⋅(sinx+cosx)2+C
c. ex⋅(sinx−cosx)2+C
d. ex⋅(cosx−sinx)2+C
Phản hồi

The correct answer is: ex⋅(sinx−cosx)2+C

3TCc719

Select one:
a. 1
b. 2
c. 3
d. 4
Phản hồi

The correct answer is: 4

3TCc705

Select one:
a. – 1
b. 3
c. – 3
d. 1
Phản hồi

The correct answer is: 1

3TCc716

Select one:
a. π/4
b. π/3
c. π/2
d. π
Phản hồi

The correct answer is: π/4

3TCc712.PNG

Select one:
a. 19/15
b. 21/23
c. 11/15
d. 24/23
Phản hồi

The correct answer is: 11/15

3TCc706.PNG

Select one:
a. 2/3
b. 10/3
c. 1
d. 4/3
Phản hồi

The correct answer is: 10/3

3TCc717.PNG

Select one:
a. 2+5/e
b. 2-5/e
c. 3/e
d. 2
Phản hồi

The correct answer is: 2-5/e

Tích phân

I=∫π20(esinx+cosx).cosxdx.

có giá trị là:

Select one:
a. e+π4−1
b. e+π4+1
c. e−π4+1
d. e+π4+2
Phản hồi
a

The correct answer is: e+π4−1

3TCc714.PNG

Select one:
a. π/4
b. 2π/3
c. 3π/8
d. π/2
Phản hồi

The correct answer is: 3π/8

3TCc707.PNG

Select one:
a. 1/3
b. (-1)/3
c. 1
d. – 1
Phản hồi

The correct answer is: 1/3

3TCc718.PNG

Select one:
a. 4e3−227
b. 4e3+227
c. 5e3−227
d. 5e3+227
Phản hồi

The correct answer is: 5e3−227

3TCc709.PNG

Select one:
a. 3√2
b. 5√2
c. 4√3
d. 4√2
Phản hồi

The correct answer is: 4√2

3TCc711.PNG

Select one:
a. 1/9
b. 2/11
c. 3/13
d. 4/15
Phản hồi

The correct answer is: 4/15

3TCc713.PNG

Select one:
a. ln2−12
b. ln2+12
c. ln3−12
d. ln3+12
Phản hồi

The correct answers are: ln2−12, ln3+12

3TCc704.PNG

Select one:
a. 1
b. 2
c. 2/3
d. 3/2
Phản hồi

The correct answer is: 2/3

3TCc708.PNG

Select one:
a. 1+2/e
b. 1-2/e
c. 2+3/e
d. 2-3/e
Phản hồi

The correct answer is: 1-2/e

3TCc720

Select one:
a. 1+ln⁡(e+1)+ln⁡2
b. 1-ln⁡(e+1)+ln⁡2
c. 1-ln⁡(e+1)-ln⁡2
d. -1+ln⁡(e+1)-ln⁡2
Phản hồi

The correct answer is: 1-ln⁡(e+1)+ln⁡2

3TCc710.PNG

Select one:
a. ln⁡(5/6)
b. ln⁡(2/3)
c. ln⁡(4/3)
d. ln⁡(3/2)
Phản hồi

The correct answer is: ln⁡(4/3)

3TCc703.PNG

Select one:
a. 2
b. 7/4
c. 3/2
d. 5/4
Phản hồi

The correct answer is: 7/4

3TCc702.PNG

Select one:
a. 4
b. – 4
c. 10
d. – 10
Phản hồi

The correct answer is: – 4

3TCc721.PNG

Select one:
a. 2/5
b. 2/15
c. 3/5
d. 3/15
Phản hồi

The correct answer is: 2/15

3TCc701.PNG

Select one:
a. – 34
b. – 2
c. – 14
d. 2
Phản hồi

The correct answer is: – 2

3TCc715.PNG

Select one:
a. 1/12
b. π/8
c. π/8+1/12
d. π/8-1/12
Phản hồi

The correct answer is: π/8-1/12

3TCc722.PNG

Select one:
a. 2ln⁡2+3/4
b. 2ln⁡2+2/3
c. 2ln⁡2-3/4
d. 2ln⁡2-2/3
Phản hồi

The correct answer is: 2ln⁡2-3/4

Tính ∫π0xsinx2dx.

Select one:

a. 1

b. 2

c. 3

d. 4

Phản hồi

Đáp án đúng là: 4.

Vì: Áp dụng công thức tích phân từng phần, đặt

{udv==xsinx2dx⇒{duv==dx−2cosx2

I=(−2x⋅cosx2)∣∣π0+2∫π0cosx2dx

I=0+(4⋅sinx2)∣∣π0=4

Tham khảo: Mục 7. 4. Phương pháp tích phân tùng phần (BG, tr. 89 ) và Mục 6. 4. 4. Phương pháp tích phân từng phần (BG, tr. 79).

The correct answer is: 4

Miền xác định của hàm số w=1−x2−2y2−−−−−−−−−−√ là:

Select one:

a. với mọi (x,y)

b. {(x,y):1−x2−2y2≠0}

c. {(x,y):1−x2−2y2=0}

d. {(x,y):1−x2−2y2≥0}

Phản hồi

Đáp án đúng là: {(x,y):1−x2−2y2≥0}.

Vì: Biểu thức chứa căn bậc 2 có nghĩa khi biểu thức bên trong căn đó phải lớn hơn hoặc bằng 0.

Tham khảo: Mục 4. 1. 2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: {(x,y):1−x2−2y2≥0}

Cho hàm số y=2×3−5×2+x−4. Đạo hàm y′(1) có giá trị là:

Select one:

a. −6

b. −3

c. −4

d. 3

Phản hồi

Đáp án đúng là: –3.

Vì: Ta có: y′=6×2−10x+1 => y′=6.12−10.1+1=−3.

Tham khảo: Mục 2.3.1. Đạo hàm của tổng, hiệu, tích, thương các hàm số (BG, tr.21).

The correct answer is: −3

Cho hàm số y=(−3x+5).e2x2−x+1. Hàm số tăng trên:

Select one:

a. (23−145√24,23+145√24)

b. (−23−145√24,−23+145√24)

c. (−∞,23−145√24) và (23+145√24,+∞)

d. (−∞,−23−145√24) và (−23+145√24,+∞)

Phản hồi

The correct answer is: (23−145√24,23+145√24)

Giả sử hàm cung và hàm cầu đối với một loại hàng hóa lần lượt là: Qs=2p2−3p+1;Qd=25−p. Mức giá cân bằng là:

Select one:

a. p0=14

b. p0=4

c. p0=3

d. p0=24

Phản hồi

Đáp án đúng là: p0=4.

Vì: Cho Qs=Qd.

2p2−3p+1=25−p⇔2p2−2p−24=0.

Δ=(−1)2−4.(−12)=49.

Phương trình có 2 nghiệm p1=−3 (loại vì p>0 và nghiệm p2=4.

Vậy mức giá cân bằng là p=4.

The correct answer is: p0=4

Giả sử một doanh nghiệp có hàm sản xuất là Q=20L−−√ . Sản phẩm hiện vật cận biên của lao động tại mức L=9 (đơn vị lao động) là:

Select one:

a. 60

b. 20

c. 10/3

d. 20/3

Phản hồi

Đúng. Đáp án đúng là: 10/3

Vì: Q′=20/(2L−−√)=10/L−−√ ⇒ Q′(9)=10/3.

Tham khảo: Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36).

The correct answer is: 10/3

Cho hàm số y=x−−√.e−2x . Khoảng tăng của hàm số là:

Select one:

a. R

b. (0,14)

c. (14,+∞)

d. (0,+∞)

Phản hồi

The correct answer is: (0,14)

Tính tích phân: I=∫cos4x.dx

Select one:

a. 38x+14sin2x+132sin4x+C

b. 38x−14sin2x+116sin4x+C

c. 38x−14sin2x−116sin4x+C

d. −38x+14sin2x+116sin4x+C

Phản hồi

Đáp án đúng là: 38x+14sin2x+132sin4x+C

Vì: Sử dụng công thức biến đổi lượng giác: cos2a=1+cos2a2.

I=∫cos4xdx=∫[38+12cos2x+18cos4x]⋅dx=38x+14sin2x+132sin4x+C

Tham khảo: Mục 6. 4. 1. Phương pháp khai triển (BG, tr. 73) và Mục 6. 4. 2. Sử dụng tính bất biến của tích phân (BG, tr. 74).

The correct answer is: 38x+14sin2x+132sin4x+C

Hàm số w=x2+2xy−y2+3x có điểm dừng là:

Select one:

a. M0(−34;−34)

b. M0(34;34)

c. M0(−34;34)

d. M0(34;−34)

Phản hồi

Đáp án đúng là: M0(−34;−34).

Vì: w′x=2x+2y+3;w′y=2x−2y, giải hệ:

{w′x=0w′y=0⇔{2x2x+−2y2y+3==00⇔{x=y4x+3=0⇒x=y=−34

Tham khảo: Mục 5.1.2. Điều kiện cần của cực trị (BG, tr. 60).

The correct answer is: M0(−34;−34)

Tính tích phân I=∫x2dx(x+2)2(x+1).

Select one:

a. 1x+1+ln|x+2|+C

b. 2x+1+ln|x+1|+C

c. ln|x+1|+4x+2+C

d. ln|x+1|−4x+2+C

Phản hồi

Đáp án đúng là: 4x+2+ln|x+1|+C.

Vì:

∫x2⋅dx(x+2)2⋅(x+1)=∫[1x+1−4(x+2)2]⋅dx=ln|x+1|+4x+2+C

Tham khảo: Mục 6.4.1. Phương pháp khai triển (BG, tr. 73) và Mục 6.3. Các công thức tích phân cơ bản (BG, tr. 73).

The correct answer is: ln|x+1|+4x+2+C

Hàm số w=f(x,y) có các đạo hàm riêng là w′x=2mx+y−3;w′y=x−5 trong đó m là tham số. Điểm M0(5,−1) là điểm dừng của hàm số w khi m có giá trị là:

Select one:

a. 5/2

b. 5

c. 2/5

d. −5

Phản hồi

Đáp án đúng là: 2/5.

Vì: Thay x=5,y=−1 , tìm m để 2 đạo hàm riêng đều triệt tiêu. 2.5.m+(−1)−3=05−5=0⇔m=25.

Tham khảo: Mục 5.1.2. Điều kiện cần của cực trị (BG, tr.60).

The correct answer is: 2/5

Xét bài toán: Giả sử doanh nghiệp cạnh tranh thuần tuý sản xuất 2 loại sản phẩm với hàm chi phí kết hợp: TC=4Q21+2Q1Q2+3Q22+5. Với giá thị trường của sản phẩm 1 là $40 và giá của sản phẩm 2 là $35, hãy chọn một cơ cấu sản lượng Q1,Q2 để hàm lợi nhuận đạt giá trị tối đa. Để giải bài toán thông qua việc tìm cực trị của hàm số, ta sẽ tìm cực đại của hàm lợi nhuận:

Select one:

a. π=35Q1+40Q2−(4Q21+2Q1Q2+3Q22+5)

b. π=35Q1+40Q2+(4Q21+2Q1Q2+3Q22+5)

c. π=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5)

d. π=40Q1+35Q2+(4Q21+2Q1Q2+3Q22+5)

Phản hồi

Đáp án đúng là: π=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5).

Vì: Doanh thu của doanh nghiệp là TR=40Q1+35Q2 =TR−TC=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5).

Tham khảo: Mục 5.2.1. Chọn mức sản lượng tối ưu (BG, tr.63).

The correct answer is: π=40Q1+35Q2−(4Q21+2Q1Q2+3Q22+5)

Cho hàm số y=e−4×2+3x+1x−1 . Số điểm tới hạn của hàm số là:

Select one:

a. 0

b. 1

c. 2

d. 3

Phản hồi

The correct answer is: 0

Tính tích phân:I=∫cosx.cos2x.cos3x.dx.

Select one:

a. 14x+18sin2x+116sin4x+124sin6x+C

b. 12x−14sin2x+sin4x−cos6x+C

c. x−cos2x−sin4x+cos6x+C

d. 14x−18sin2x−116sin4x+124sin6x+C

Phản hồi

The correct answer is: 14x+18sin2x+116sin4x+124sin6x+C

Tính ∫10x2e−xdx.

Select one:

a. 2+5/e

b. 2−5/e

c. 3/e

d. 2

Phản hồi

Đáp án đúng là: 2−5e.

Vì: Áp dụng công thức tích phân từng phần, đặt

{udv==x2e−x.dx⇒{du=2x⋅dxv=−e−xI=(−x⋅e−x)∣∣10+2∫10x⋅e−x.dx=−1e+2∫10x⋅e−x⋅dxJ

Tính J, đặt

{udv==xe−xdx⇒{du=dxv=−e−xJ=∫10x⋅e−x⋅dx=(−xex)∣∣∣10+∫10e−x⋅dx=1−2e⇒I=−1e+2(1−2e)=2−5e

Tham khảo: Mục 7.4. Phương pháp tích phân từng phần (BG, tr. 89 ) và Mục 6. 4. 4. Phương pháp tích phân từng phần (BG, tr.79).

The correct answer is: 2−5/e

Cho hàm số y=x.4−3x−−−−−−√ . Giá trị lớn nhất của hàm số trên [−1,43] là:

Select one:

a. 0

b. 16/(93–√)

c. 20/(93–√)

d. 22/(93–√)

Phản hồi

The correct answer is: 16/(93–√)

Tính tích phân: ∫(x2+1)3⋅dx

Select one:

a. x77+3⋅x55+x3+x+C

b. x77−3⋅x55+x3−x+C

c. −x77+3⋅x55−x3+x+C

d. x77+3⋅x55+x3+C

Phản hồi

Đáp án đúng là: x77+3⋅x55+x3+x+C.

Vì: Sử dụng công thức tích phân cơ bản ∫(x2+1)3⋅dx=∫(x6+3×4+3×2+1)dx =x77+3⋅x55+x3+x+C.

Tham khảo: Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73).

The correct answer is: x77+3⋅x55+x3+x+C

Select one:

a. đạt giá trị cực đại.

b. đạt giá trị cực tiểu.

c. không đạt cực trị.

d. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của x0,y0.

Phản hồi

The correct answer is: đạt giá trị cực tiểu.

Đạo hàm riêng theo biến x của hàm số w=ln(4x−3y) tại điểm (1,0) là:

Select one:

a. 1/4

b. 0

c. –3/4

d. 1

Phản hồi

Đáp án đúng là: 1.

Vì: Lấy đạo hàm của hàm số theo biến x rồi thay x=1,y=0 vào tìm giá trị của biểu thức: w′x=44x−3yw′x(1,0)=44−0=1.

Tham khảo: Mục 4.4.1. Đạo hàm riêng tại một điểm (BG, tr. 51).

The correct answer is: 1

Xét bài toán tìm cực trị của hàm số w=3x+2y với điều kiện ràng buộc là phương trình 3×2+y2=7 . Sử dụng phương pháp nhân tử Lagrange với hàm Lagrange L=3x+2y+λ(7−3×2−y2) ta biết hàm số đạt giá trị cực tiểu tại điểm (x0=−1;y0=−2) ứng với λ0=−12 . Nếu điều kiện ràng buộc được thay bằng phương trình 3×2+y2=8 thì giá trị cực đại của hàm số sẽ:

Select one:

a. tăng 1 đơn vị.

b. giảm 2 đơn vị.

c. giảm 1/2 đơn vị.

d. tăng 1/2 đơn vị.

Phản hồi

Đáp án đúng là: giảm 12 đơn vị.

Vì: Theo ý nghĩa của nhân tử Lagrange: dw¯¯¯¯db=λ¯¯¯.

Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: giảm 1/2 đơn vị.

Cho y=ex√. Đạo hàm cấp 2 của y là:

Select one:

a. y′′=ex√4(1x−x−−√)

b. y′′=ex√

c. y′′=ex√4(1x−1x√3)

d. y′′=ex√4(1x√3−1x)

Phản hồi

Đáp án đúng là: y′′=ex√4(1x−1×3√).

Vì: Đạo hàm cấp 1 là

y′=ex√⋅(x−−√)′=ex√⋅12x√

Tiếp tục tính đạo hàm cấp 2:

y′′=(y′)′=(ex√)′12x−−√+ex√⋅(12x−−√)′=ex√.(x−−√)′⋅12x−−√+ex√⋅−(x−−√)′2x=ex√⋅12x−−√⋅12x−−√+ex√−12x−−√⋅2x=ex√4(1x−1xx−−√)=ex√4(1x−1×3−−√)

Tham khảo: Mục 2. 5. 1. Đạo hàm cấp cao (BG, tr. 25).

The correct answer is: y′′=ex√4(1x−1x√3)

Tính tích phân: I=∫(x2−2x+4x).dx

Select one:

a. x33+x2−4ln|x|+C

b. x33−x2+4ln|x|+C

c. 2x−2−4×2+C

d. 2x+2+4×2+C

Phản hồi

Đáp án đúng là: x33−x2+4ln|x|+C.

Vì: Khai triển tích phân và áp dụng các công thức tích phân cơ bản ta được kết quả I=∫(x2−2x+4x).dx=\intx2.dx−2.\intx.dx+4.∫dxx=x33−x2+4ln|x|+C.

Tham khảo: Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73).

The correct answer is: x33−x2+4ln|x|+C

Tính tích phân: I=∫dxx1+lnx−−−−−−√

Select one:

a. 1+lnx+C

b. 1+lnx−−−−−−√

c. 21+lnx−−−−−−√

d. 1+2lnx−−−−−−−−√.

Phản hồi

Đáp án đúng là: 21+lnx−−−−−−√.

Vì: Nhận xét thấy (1+lnx)′=1x.

Viết tích phân dưới dạng:

I=∫d(1+lnx)1+lnx−−−−−−√.

Từ đó ta tính được:

I=21+lnx−−−−−−√+C.

Tham khảo: Mục 6. 4. 2. Sử dụng tính bất biến của tích phân (BG, tr. 74).

The correct answer is: 21+lnx−−−−−−√

Cho hàm số y=(5x−3)2.(4−7x)3 . Số điểm dừng nhưng không phải là điểm cực trị của hàm số là:

Select one:

a. 1

b. 2

c. 3

d. 4

Phản hồi

The correct answer is: 1

Select one:

a. là điểm cực đại của hàm số.

b. là điểm cực tiểu của hàm số.

c. không là điểm cực trị của hàm số.

d. có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.

Phản hồi

Đáp án đúng là: không là điểm cực trị của hàm số.

Vì: Tìm các đạo hàm riêng cấp 2 của hàm số w, xét điều kiện đủ thấy D<0.

Cụ thể:

w′′xx=(w′x)′x=6x;w′′xy=w′′yx=(w′y)′x=−2;w′′yy=(w′y)′y=2D=∣∣∣−2−2−22∣∣∣=−4−4=−8<0

Tham khảo: Mục 5. 1. 3. Điều kiện đủ của cực trị (BG, tr. 60).

The correct answer is: không là điểm cực trị của hàm số.

Cho hàm số y=x3−4×2+5x−2 . Giá trị nhỏ nhất của hàm số trên [0,2] là:

Select one:

a. −3

b. −2

c. 0

d. 1

Phản hồi

Đáp án đúng là: −2.

Vì: y′=3×2−8x+5.

Giải phương trình y′=0 ta được 2 nghiệm là 1 và 5/3.

Tính giá trị của hàm số tại hai điểm dừng và tại các đầu mút của đoạn đang xét: y(0),y(2),y(1) và y(5/3).

Ta có: y(0)=−2;y(1)=0;y(53)=−427;y(2)=0.

So sánh các giá trị ta thấy miny[0,2]=y(0)=−2.

Như vậy, y đạt giá trị nhỏ nhất tại x=0.

Tham khảo: Mục 3.2.5. Bài toán cực trị toàn thể (BG, tr. 36).

The correct answer is: −2

Cho hàm số y=2×3−3×2+9. Số điểm cực trị của hàm số là:

Select one:

a. 4

b. 3

c. 2

d. 1

Phản hồi

The correct answer is: 2

Select one:

a. 1

b. 2

c. –1/2

d. 1/2

Phản hồi

Đáp án đúng là: 12.

Vì: Thay x=2 vào phương trình L′x=0 tìm được giá trị của λ0 . Ta có: 2−2.λ.2=0⇒λ=12.

Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: 1/2

Tính tích phân:I=∫x.ex(x+1)2dx

Select one:

a. xexx+1+ex+C

b. −xexx+1+2ex+C

c. exx+1+C

d. −exx+1+C

Phản hồi

The correct answer is: exx+1+C

Tính ∫10×31−x2−−−−−√dx.

Select one:

a. 25

b. 215

c. 35

d. 315

Phản hồi

Đáp án đúng là: 215.

Vì: Sử dụng cách đặt

t=1−x2−−−−−√⇒x2=1−t2;xdx=−tdt.

I=∫10(t2−t4)dt=(t33−t55)∣∣∣10=215.

Tham khảo: Mục 7. 3. Phương pháp đổi biến (BG, tr. 88).

The correct answer is: 215

Select one:

a. L=x0,4y0,5+λ(200−4x−5y)

b. L=x0,4y0,5+λ(200+4x+5y)

c. L=x0,4y0,5+λ(200−4x+5y)

d. L=x0,4y0,5+λ(200+4x−5y)

Phản hồi

Đáp án đúng là: L=x0,4y0,5+λ(200−4x−5y).

Vì: Điều kiện ràng buộc ngân sách là 4x+5y=200.

Tham khảo: Mục 5.4. Ứng dụng trong kinh tế học: Bài toán tối đa hóa lợi ích tiêu dùng (BG, tr.66).

The correct answer is: L=x0,4y0,5+λ(200−4x−5y)

Miền xác định của hàm số w=3x+2ln(x−2y) là:

Select one:

a. với mọi (x,y)

b. {(x,y):x−2y≥0}

c. {(x,y):x−2y≠0}

d. {(x,y):x−2y>0}

Phản hồi

Đáp án đúng là: {(x,y):x−2y>0}.

Vì: Biểu thức bên trong logarit phải lớn hơn 0.

Tham khảo: Mục 4.1.2. Miền xác định của hàm số cho dưới dạng biểu thức (BG, tr. 46 – 47).

The correct answer is: {(x,y):x−2y>0}

Tính ∫10dxex+1.

Select one:

a. 1+ln(e+1)+ln2

b. 1−ln(e+1)+ln2

c. 1−ln(e+1)−ln2

d. −1+ln(e+1)−ln2

Phản hồi

Đáp án đúng là: 1−ln(e+1)+ln2

Vì: Đặt

t=ex⇒I=∫e1dtt⋅(t+1)=∫e1(1t−1t+1)dt

I=[lnt−ln(t+1)]∣∣e1=1−ln(e+1)+ln2

Tham khảo: Mục 7. 3. Phương pháp đổi biến (BG, tr. 88).

The correct answer is: 1−ln(e+1)+ln2

Đạo hàm riêng theo biến x của hàm số w=y2+yx+x−−√ là:

Select one:

a. w′x=yx2+12x√

b. w′x=−yx2+12x√

c. w′x=4×3+4xy−3cosx

d. w′x=2×2+12y√

Phản hồi

Đáp án đúng là: w′x=−yx2+12x√.

Vì: Lấy đạo hàm của hàm số theo biến x (coi y là hằng số\). Chú ý: (1x)′x=−1x2và(x−−√)′=12x√.

Tham khảo: Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).

The correct answer is: w′x=−yx2+12x√

Cho hàm f(x)=x−−√,g(x)=ex(x−1). Đạo hàm của hàm h(x)=g(f(x)) là:

Select one:

a. ex√(x−−√−1).

b. 12x√ex√.

c. ex(x−1)−−−−−−−−√.

d. 12ex√.

Phản hồi

Đáp án đúng là: 12ex√.

Vì: Tính đạo hàm của hàm h(x) theo công thức đạo hàm hàm hợp hoặc lập hàm h(x) rồi tính đạo hàm. Cụ thể là:

g′(x)h′(x)=ex(x−1)+ex=xex;f′(x)=12x−−√=g′(f(x))⋅f′(x)=x−−√ex√⋅12x−−√=12ex√.

Tham khảo: Mục 2. 3. 2. Đạo hàm của hàm hợp (BG, tr. 22)

The correct answer is: 12ex√.

Xét hàm số hai biến số w=f(x,y). Ký hiệu: D=∣∣∣a11a21a12a22∣∣∣=a11.a22−a12.a21 với a11,a12,a21,a22 lần lượt là giá trị của các đạo hàm riêng cấp 2 w′′xx,w′′xy,w′′yx,w′′yy tính tại điểm dừng M0(x0,y0). Khi đó nếu D>0 thì theo điều kiện đủ của cực trị, điểm M0(x0,y0):

Select one:

a. là điểm cực đại của hàm số.

b. là điểm cực tiểu của hàm số.

c. không là điểm cực trị của hàm số.

d. là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a11.

Phản hồi

Đáp án đúng: là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a11.

Vì: Theo điều kiện đủ của cực trị.

Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị (BG, tr.60).

The correct answer is: là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a11.

Tính tích phân: I=∫tan2x⋅dx

Select one:

a. tan2x−2x+C

b. tan2x+2x+C

c. tanx−x+C

d. tanx+x+C

Phản hồi

Đáp án đúng là: tanx−x+C.

Vì: I=∫tan2x⋅dx=∫(1cos2x−1)⋅dx=tanx−x+C.

Tham khảo: Mục 6.4.1. Phương pháp khai triển (BG, tr.73) và mục 6.3. Các công thức tích phân cơ bản (BG, tr.73).

The correct answer is: tanx−x+C

Tính ∫411+x−−√x2dx

Select one:

a. 2

b. 74

c. 32

d. 54

Phản hồi

Đáp án đúng là: 74.

Vì: Sử dụng phương pháp khai triển

∫411+x−−√x2dx=∫41(1×2+x−−√x2)dx=(−1x+−2x−−√)∣∣∣41=74.

Tham khảo: Mục 7.2. Các tính chất cơ bản của tích phân xác định (BG, tr. 87).

The correct answer is: 74

Giả sử doanh nghiệp hoạt động trong thị trường cạnh tranh với hàm sản xuất ngắn hạn là Q=30L−−√. Cho biết giá mỗi đơn vị sản phẩm là p=$2, giá thuê một đơn vị lao động là wL=$5 và chi phí cố định C0=15. Tại mức sử dụng 9 đơn vị lao động, lợi nhuận của doanh nghiệp là:

Select one:

a. π=$15

b. π=$45

c. π=$135

d. π=$120

Phản hồi

Đáp án đúng là: π=$120.

Vì: Tại L=9, sản lượng là Q=90, doanh thu là TR=p.Q=2.90=180. Chi phí thuê lao động là TC=5.9=45. Suy ra lợi nhuận π=180−(45+15)=120.

Tham khảo: Mục 1.7.3. Hàm doanh thu, hàm chi phí và hàm lợi nhuận (BG, tr.13).

The correct answer is: π=$120

Select one:

a. 1

b. 2

c. −1/4

d. 1/2

Phản hồi

Đáp án đúng là: −14.

Vì: Thay y=−2 vào phương trình L′y=0 tìm được giá trị của λ0 . Ta có: 3−6.λ.(−2)=0⇒λ=−14.

Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: −1/4

Select one:

a. D=∣∣∣a11a21a12a22∣∣∣

b. D=∣∣∣a11a12a22a21∣∣∣

c. D=∣∣∣a11a21a22a12∣∣∣

d. D=∣∣∣a11a21a12a11∣∣∣

Phản hồi

Đáp án đúng là: D=∣∣∣a11a21a12a22∣∣∣.

Vì: theo điều kiện đủ của cực trị.

Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị.

The correct answer is: D=∣∣∣a11a21a12a22∣∣∣

Cho hàm số y=13×3−2×2+4x+3 . Số điểm cực trị của hàm số là:

Select one:

a. 0

b. 1

c. 2

d. 3

Phản hồi

Đáp án đúng: Hàm số không có cực trị.

Vì: y′=x2−4x+4=(x−2)2. Giải y′=0 ta được 1 nghiệm y′=0⇔x2−4x+4=0⇔x=2 y′≥0,∀x. ⇒ Hàm số không có cực trị.

Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 0

|H¯¯¯¯¯|=∣∣∣∣012101210∣∣∣∣

Khi đó, ta kết luận được: tại điểm (x0,y0) hàm số

Select one:

a. đạt giá trị cực đại.

b. đạt giá trị cực tiểu.

c. không đạt cực trị.

d. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của λ0.

Phản hồi

Đáp án đúng là: đạt giá trị cực đại.

Vì: Tính định thức cấp 3: |H¯¯¯¯¯|=0+2+2−(0+0+0)=4>0.

Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: đạt giá trị cực đại.

Tinh tích phân:

∫ex⋅dxex+1

Select one:

a. 2ln(ex+1)+C

b. −2ln(ex+1)+C

c. −ln(ex+1)+C

d. ln(ex+1)+C

Phản hồi

Đáp án đúng là: ln(ex+1)+C.

Vì: ∫ex⋅dxex+1=∫d(ex+1)ex+1=ln(ex+1)+C.

Tham khảo: Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74).

The correct answer is: ln(ex+1)+C

Cho hàm số y=x.e2x. Vi phân của hàm số tại điểm x0=12 với số gia Δx=0,1 có giá trị là:

Select one:

a. 0,2e

b. 0,1e

c. 0,3e

d. 1,5e

Phản hồi

Đáp án đúng là: 0,2e

Vì: Ta có :

y′=(xe2x)′=x′⋅e2x+x⋅(e2x)′=e2x+2xe2x=(1+2x)e2x⇒y′(12)=(1+2⋅12)⋅e2⋅12=2e⇒df(12)=y′(12)⋅Δx=2e⋅0,1=0,2e

Tham khảo: Mục 2.4.1. Khái niệm vi phân và biểu thức vi phân (BG, tr. 24).

The correct answer is: 0,2e

Cho hàm số y=x−1−−−−−√⋅3−x−−−−−√+x2−4x+3−−−−−−−−−−√ Tập xác định của hàm số là:

Select one:

a. {1,3}

b. (−∞,1)∪(3,+∞)

c. R

d. (1,3)

Phản hồi

Đáp án đúng là: {1,3}

Vì: Điều kiện xác định là

⎧⎩⎨⎪⎪x−1≥03−x≥0x2−4x+3≥0⇔⎧⎩⎨⎪⎪x≥1x≤3×2−4x+3≥0

Giải bất phương trình thứ 3: x2−4x+3≥0.

Tam thức bậc 2: P(x)=x2−4x+3 có a+b+c=1−4+3=0 nên có 2 nghiệm là 1 và 3.

Xét dấu P(x) ta có nghiệm của bất phương trình thứ 3 là: [x≤1x≥3

Từ đó suy ra nghiệm của hệ 3 bất phương trình là: x=1 hoặc x=3.

Tập xác định gồm 2 giá trị: D={1;3}.

Tham khảo: Mục 1.2.2. Hàm số cho dưới dạng biểu thức (BG, tr. 4).

The correct answer is: {1,3}

Xét hàm số hai biến số w=f(x,y). Ký hiệu: D=∣∣∣a11a21a12a22∣∣∣=a11.a22−a12.a21 với a11,a12,a21,a22 lần lượt là giá trị của các đạo hàm riêng cấp 2 w′′xx,w′′xy,w′′yx,w′′yy tính tại điểm dừng M0(x0,y0). Khi đó, điều kiện đủ để điểm M0(x0,y0) là điểm cực đại của hàm số w là:

Select one:

a. D<0

b. D>0;a11>0

c. D>0;a11<0

d. D=0

Phản hồi

Đáp án đúng là: D>0;a11<0.

Theo điều kiện đủ để hàm số 2 biến số dạt giá trị cực đại.

The correct answer is: D>0;a11<0

Hàm số w=f(x,y) có các đạo hàm riêng là w′x=2x+my−3;w′y=mx−6y−5 trong đó m là tham số. Điểm M0(1,−1) là điểm dừng của hàm số w khi m có giá trị là:

Select one:

a. -1

b. 1

c. 0

d. 1/2

Phản hồi

The correct answer is: -1

Tính tích phân: I=∫x.lnx.dx

Select one:

a. −12x2lnx−14×2+C

b. 12x2lnx−14×2+C

c. x2lnx−12×2+C

d. x2lnx+12×2+C

Phản hồi

The correct answer is: 12x2lnx−14×2+C

Tính ∫π0cos4xdx.

Select one:

a. π/4

b. 2π/3

c. 3π/8

d. π/2

Phản hồi

Đáp án đúng là: 3π8

Vì: Sử dụng công thức biến đổi lượng giác, sau đó tính tích phân và thay số:

∫π0cos4x⋅dx=∫π0(38+12cos2x+18cos4x)⋅dx

=(38x+14sin2x+132sin4x)∣∣∣π0=3π8.

Tham khảo: Mục 7.2. Các tính chất cơ bản của tích phân xác định (BG, tr.87).

The correct answer is: 3π/8

Tính tích phân}: ∫x2dxx3+1−−−−−√

Select one:

a. x3+1−−−−−√+C

b. – x3+1−−−−−√+C

c. −23×3+1−−−−−√+C

d. 23×3+1−−−−−√+C

Phản hồi

Đáp án đúng là: 23×3+1−−−−−√+C.

Vì: ∫x2dxx3+1−−−−−√=13∫d(x3+1)x3+1−−−−−√=23×3+1−−−−−√+C.

Tham khảo: Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74).

The correct answer is: 23×3+1−−−−−√+C

Tính ∫30dx25−3x−−−−−−√.

Select one:

a. 1

b. 2

c. 2/3

d. 3/2

Phản hồi

Đáp án đúng là: 23.

Vì: Sử dụng tính bất biến của tích phân

∫30dx25−3x−−−−−−√=−13∫30d(25−3x)25−3x−−−−−−√=(−23⋅25−3x−−−−−−√)∣∣∣30=23

Tham khảo: Mục 7.2. Các tính chất cơ bản của tích phân xác định (BG, tr. 87).

The correct answer is: 2/3

Hàm số w=x0,2y0,5 có đạo hàm riêng cấp 2 w′′xy là:

Select one:

a. 0,2x−0,8y0,5

b. 0,1×0,8y0,5

c. −0,1x−0,8y−0,5

d. 0,1x−0,8y−0,5

Phản hồi

Đáp án đúng là: 0,1x−0,8y−0,5.

Vì: w′x=0,2x−0,8y0,5. Tiếp tục lấy đạo hàm theo y: w′′xy=(w′x)′y=0,2.0,5x−0,8y−0,5=0,1x−0,8y−0,5.

Tham khảo: Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).

The correct answer is: 0,1x−0,8y−0,5

Cho hàm số y=−3×2+4x−1−−−−−−−−−−−−√. Tập xác định của hàm số là:

Select one:

a. [13,1]

b. [13,+∞)

c. [1,+∞)

d. (−∞,13]

Phản hồi

Đáp án đúng là: [13,1].

Vì: Điều kiện để căn có nghĩa là:

−3×2+4x−1≥0

Tam thức bậc hai P(x)=−3×2+4x−1 có 2 nghiệm là 1 và 13.

Xét dấu của P(x), ta suy ra nghiệm của bất phương trình trên là: 13≤x≤1⇒ tập xác định là: D=[13,1].

Tham khảo: Mục 1.2.2. Hàm số cho dưới dạng biểu thức (BG, tr.4).

The correct answer is: [13,1]

Cho hàm số y=5×2−4cosx+3. Đạo hàm y′ là:

Select one:

a. y′=10x−4sinx

b. y′=10x−4sinx+3

c. y′=10x+4sinx

d. y′=10x+4sinx+3

Phản hồi

Đáp án đúng là: y′=10x+4sinx.

Vì (x2)′=2x;(cosx)′=−sinx;(3)′=0.

Tham khảo: Mục 2.3.1. Đạo hàm của tổng, hiệu, tích, thương các hàm số (BG, tr.21).

The correct answer is: y′=10x+4sinx

Hàm số 2 biến số w=f(x,y) có số đạo hàm riêng cấp 2 nhiều nhất là:

Select one:

a. 2

b. 4

c. 6

d. 8

Phản hồi

Đáp án đúng là: 4.

Vì: Hàm số 2 biến số {có thể có} 4 đạo hàm riêng cấp 2 là $w^{“}_{xx}, w^{“}_{xy}, w^{“}_{yx}, w^{“}_{yy}$.

Tham khảo: Mục 4.6. Đạo hàm riêng cấp 2 của hàm số 2 biến số (BG, tr. 53).

The correct answer is: 4

Cho hàm số y=x3−2×2+x+3 . Số điểm dừng của hàm số là:

Select one:

a. 1

b. 2

c. 3

d. 4

Phản hồi

Đáp án đúng là: 2.

Vì: y′=3×2−4x+1. Giải y′=0: y′=3×2−4x+1=0⇔x1=1;x2=13.

Như vậy, hàm số có hai điểm dừng là: x1=1;x2=13.

Tham khảo: Mục 3. 2. 2. Điều kiện cần của cực trị (BG, tr. 34).

The correct answer is: 2

Tính tích phân: ∫3x+22×2+x−3⋅dx

Select one:

a. ln|x−1|+2ln|2x+3|+C

b. ln|x−1|−2ln|2x+3|+C

c. −ln|x−1|+ln|2x+3|+C

d. ln|x−1|+12ln|2x+3|+C

Phản hồi

Đáp án đúng là: ln|x−1|+12ln|2x+3|+C.

Vì: Sử dụng phương pháp khai triển:

∫3x+22×2+x−3dx=∫(1x−1+12x+3)dx=ln|x−1|+12ln|2x+3|+C.

Tham khảo: Mục 6. 4. 1. Phương pháp khai triển (BG, tr. 73) và Mục 6. 3. Các công thức cơ bản (BG, tr. 73).

The correct answer is: ln|x−1|+12ln|2x+3|+C

Cho hàm số y=(3×3−5x+1).sinx. Đạo hàm y′ là:

Select one:

a. y′=(9×2−5)sinx

b. y′=(9×2−5)sinx+(3×3−5x+1)cosx

c. y′=(9×2−5)cosx

d. y′=(3×3−5x+1)cosx

Phản hồi

Đáp án đúng là: y′=(9×2−5)sinx+(3×3−5x+1)cosx.

Vì: Đây là đạo hàm tích u.v với u=(3×3−5x+1);v=sinx ⇒y′=(3×3−5x+1)′sinx++(3×3−5x+1)(sinx)′ =(9×2−5)sinx+(3×3−5x+1)cosx.

Tham khảo: Mục 2.3.1. Đạo hàm của tổng, hiệu, tích, thương các hàm số (BG, tr.21).

The correct answer is: y′=(9×2−5)sinx+(3×3−5x+1)cosx

Đạo hàm riêng theo biến y của hàm số w=x4+x2y−sinx+2y√ là:

Select one:

a. 4×3+2xy−cosx

b. 4×3+x2+2y√

c. x2+2y√

d. x2+1y√

Phản hồi

Đáp án đúng là: x2+1y√.

Vì: Lấy đạo hàm của hàm số theo biến y (coi x là hằng số). Chú ý: (y√)′y=12y√.

Tham khảo: Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).

The correct answer is: x2+1y√

Biểu thức vi phân của hàm số y=xx,x>0 là:

Select one:

a. dy=x.xx−1dx

b. dy=xx.lnx.dx

c. dy=xx.(1+lnx).dx

d. dy=xxdx

Phản hồi

Đáp án đúng là: dy=xx(1+lnx).dx.

Vì: Sử dụng phương pháp logarit hoá để tính đạo hàm. Lấy ln hai vế ta được lny=xlnx. Sau đó, đạo hàm 2 vế:

(lny)′=(xlnx)′

y′y=x′lnx+x(lnx)′=lnx+x×1x=lnx+1.

⇒y′=y(1+lnx)=xx(1+lnx)

dy=y′dx=xx(1+lnx)dx

Tham khảo: Mục 2. 3. 3. Đạo hàm của biểu thức lũy thừa mũ và phương pháp logarit hóa (BG, tr. 23).

The correct answer is: dy=xx.(1+lnx).dx

Cho hàm lợi nhuận phụ thuộc vào mức sản lượng của một doanh nghiệp là: π=−Q3+15Q2+600Q+800 Lợi nhuận tối đa của doanh nghiệp là:

Select one:

a. 6800

b. 9800

c. 11800

d. 10800

Phản hồi

The correct answer is: 10800

Cho hàm số y=5−4x−−−−−−√3 . Kết luận đúng về hàm số là:

Select one:

a. Hàm số không đạt cực đại.

b. Hàm số đạt giá trị cực đại tại x=1

c. Hàm số đạt giá trị cực đại tại x=2

d. Hàm số đạt giá trị cực đại tại x=5/4

Phản hồi

Đáp án đúng: Hàm số không đạt cực đại.

Vì: y′=−43(5−4x)2√3<0. Do đó y không đạt cực trị.

Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: Hàm số không đạt cực đại.

Cho hàm số y=esinx−sinx . Số điểm dừng của hàm số trên [−π2,π] là:

Select one:

a. 1

b. 2

c. 3

d. 4

Phản hồi

The correct answer is: 4

Select one:

a. là điểm cực đại của hàm số.

b. là điểm cực tiểu của hàm số.

c. không là điểm cực trị của hàm số.

d. có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.

Phản hồi

The correct answer is: là điểm cực tiểu của hàm số.

Tính tích phân: I=∫e8x.dx

Select one:

a. 18e8x+C

b. 8e8x+C

c. e8x+C

d. −e8x+C

Phản hồi

Đáp án đúng là: 18e8x+C.

Vì: I=∫e8x.dx=18∫e8x.d(8x)=18e8x+C.

Tham khảo: Mục 6.4.2. Sử dụng tính bất biến của tích phân (BG, tr.74).

The correct answer is: 18e8x+C

Cho ∫30f(x)dx=9 và ∫40f(z)dz=5. Kết quả của tích phân I=∫43f(t)dt là:

Select one:

a. 4

b. –4

c. 10

d. –10

Phản hồi

Đáp án đúng là: −4.

Vì: Áp dụng tính chất của tích phân:

∫43f(t)dt=∫40f(t)dt−∫30f(t)dt=5−9=−4.

Tham khảo: Mục 7.2. Các tính chất cơ bản của tích phân xác định (BG, tr. 87).

The correct answer is: –4

Tính ∫40xdx2x+1−−−−−−√.

Select one:

a. 2/3

b. 10/3

c. 1

d. 4/3

Phản hồi

Đáp án đúng là: 103.

Vì: Đặt t=2x+1−−−−−−√⇒x=t2−12⇒dx=t.dt

Đổi cận: x=0→t=1,x=4→t=3

I=∫40x⋅dx2x+1−−−−−−√=12∫31(t2−1)dt=12(t33−t)∣∣∣31=103

Tham khảo: Mục 7.3. Phương pháp đổi biến (BG, tr. 88).

The correct answer is: 10/3

Biểu thức vi phân của hàm y=x2.e−5x là

Select one:

a. dy=(2x−5×2)e−5x.dx

b. dy=2x.e−5x.dx

c. dy=−5×2.e−5x.dx

d. dy=−10x.e−5x.dx

Phản hồi

Đáp án đúng là: dy=(2x−5×2)e−5x⋅dx.

Vì:

y′=(x2⋅e−5x)′=(x2)′⋅e−5x+x2⋅(e−5x)′=2x⋅e−5x+x2⋅e−5x⋅(−5x)′=2x⋅e−5x−5×2⋅e−5x=(2x−5×2)⋅e−5x

⇒ Biểu thức vi phân là: dy=y′⋅dx=(2x−5×2)⋅e−5x⋅dx

The correct answer is: dy=(2x−5×2)e−5x.dx

Tính tích phân: I=∫(x+sinx)2⋅dx

Select one:

a. x2+2sinx−2xcosx+C

b. x33−x2−2sinx+2xcosx+14sin2x+C

c. x33+x2+2sinx−2xcosx−14sin2x+C

d. x33sinx+xcosx+C

Phản hồi

Đáp án đúng là: x33+x2+2sinx−2xcosx−14sin2x+C.

Vì: Khai triển bình phương và tách thành 3 tích phân.

I=∫(x+sinx)2⋅dx=∫(x2+2x⋅sinx+sin2x)⋅dx=x33+2∫x⋅sinx⋅dxJ+12∫(1−cos2x)⋅dxH

Tính J: Đặt

{udv==xsinx.dx⇒{duv==dx−cosx

J=2∫x.sinx.dx=−2x.cosx+2∫cosxdx=−2x⋅cosx+2sinx+C1.

Tính H :

H=12∫(1−cos2x)⋅dx=x2−14sin2x+C2

⇒I=x33+x2+2sinx−2xcosx−14sin2x+C

Tham khảo: Mục 6. 4. 4. Phương pháp tích phân từng phần (BG, tr. 79).

The correct answer is: x33+x2+2sinx−2xcosx−14sin2x+C

Cho hàm số y=e|x|√x2+1. Tập xác định của hàm số là:

Select one:

a. (0,+∞)

b. (−∞,0)

c. (−1,+∞)

d. R

Phản hồi

Đáp án đúng là: R.

Vì: Biểu thức trong căn là giá trị tuyệt đối nên luôn dương và biểu thức dưới mẫu luôn khác 0. Như vậy, hàm số xác định tại mọi giá trị thực x.

Tham khảo: Mục 1.2.2. Hàm số cho dưới dạng biểu thức (BG, tr.4).

The correct answer is: R

Tính ∫10x.e−xdx.

Select one:

a. 1+2/e

b. 1−2/e

c. 2+3/e

d. 2−3/e

Phản hồi

Đáp án đúng là: 1−2e

Vì: Đặt

{u=xdv=e−x.dx⇒{du=dxv=−e−xI=(−x,e−x)∣∣10+∫10e−x⋅dx=1−2e

Tham khảo: Mục 7.2. Các tính chất cơ bản của tích phân xác định (BG, tr. 87) và Mục 6.4 .4. phương pháp tích phân từng phần (BG, tr .79).

The correct answer is: 1−2/e

Cho hàm(x2−3x+2).e−2x. Hàm số giảm trên:

Select one:

a. (2−12√,2+12√)

b. (2+12√,+∞)

c. (−∞,2−12√)∪(2+12√,+∞)

d. 2 khoảng (−∞,2−12√) và (2+12√,+∞)

Phản hồi

The correct answer is: (−∞,2−12√)∪(2+12√,+∞)

Đạo hàm riêng theo biến x của hàm số w=3×2−2xy+y3 tại điểm (1,2) là:

Select one:

a. 14

b. 6

c. 2

d. 10

Phản hồi

Đáp án đúng là: 2.

Vì: Lấy đạo hàm của hàm số theo biến x rồi thay x=1,y=2 vào tìm giá trị: w′x=6x−2y; w′x(1,2)=6.1−2.2=2.

Tham khảo: Mục 4.4.1. Đạo hàm riêng tại một điểm (BG, tr. 51).

The correct answer is: 2

Đạo hàm của hàm số y=tan3(6x) là:

Select one:

a. y′=3tan2(6x)cos2(6x)

b. y′=3tan2(6x)

c. y′=6cos2(6x)

d. y′=18tan2(6x)cos2(6x)

Phản hồi

Đáp án đúng là: y′=18tan2(6x)cos2(6x).

Vì: Đây là đạo hàm của hàm hợp u3 với u=tan(6x)

(u3)′=3u2u′;u′=(tan(6x))′=6cos2(6x).

Do đó:

y′=3tan2(6x)×6cos2(6x)=18tan2(6x)cos2(6x)

Tham khảo: Mục 2.3.2. Đạo hàm của hàm hợp (BG, tr. 22).

The correct answer is: y′=18tan2(6x)cos2(6x)

Cho hàm số y=x−−√3. Số điểm tới hạn của hàm số là:

Select one:

a. 1

b. 2

c. 3

d. 4

Phản hồi

Đúng. Đáp án đúng là: 1.

Vì: y′=1/(3×2−−√3) nên y′ không xác định tại x=0.

Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 1

|H¯¯¯¯¯|=∣∣∣∣02−1201−110∣∣∣∣

Khi đó, ta kết luận được: tại điểm x0,y0) hàm số

Select one:

a. đạt giá trị cực đại.

b. đạt giá trị cực tiểu.

c. không đạt cực trị.

d. có thể đạt cực đại hoặc cực tiểu tùy thuộc vào giá trị của λ0.

Phản hồi

Đáp án đúng là: đạt giá trị cực tiểu.

Vì: Tính định thức cấp 3: |H¯¯¯¯¯|=0−2−2−(0+0+0)=−4<0.

Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: đạt giá trị cực tiểu.

Đạo hàm riêng theo biến x của hàm số w=x3+xy2−3x+y là:

Select one:

a. y2+1

b. 3×2+y2−2

c. 3×2+y2−3

d. 3×2+y2

Phản hồi

Đáp án đúng là: 3×2+y2−3.

Vì: Lấy đạo hàm của hàm số theo biến x: w′x=(x3)′x+y2(x)′x−3(x)′x+0=3×2+y2−3.

Tham khảo: Mục 4.4.2. Đạo hàm riêng trên một miền (BG, tr. 52).

The correct answer is: 3×2+y2−3

Cho hàm số y=2x−34−x. Đạo hàm cấp hai y′′ là:

Select one:

a. y′′=10(4−x)3

b. y′′=−4(4−x)2

c. y′′=−58−2x

d. y′′=−10(4−x)3

Phản hồi

Đáp án đúng là: y′′=10(4−x)8.

Vì: Hàm số y=2x−34−x có dạng uv; sử dụng công thức (uv)′=u′v−uv′v2.

y′=(2x−3)′⋅(4−x)−(2x−3)⋅(4−x)′(4−x)2=2(4−x)−(2x−3)(−1)(4−x)2

y′=8−2x+2x−3(4−x)2=5(4−x)2

Tiếp tục tính đạo hàm của y′, ta có:

y′′=(y′)′=[5(4−x)2]′=−5[(4−x)2]′(4−x)4=−5.2(4−x)(4−x)′(4−x)4=10(4−x)(4−x)4=10(4−x)3

Tham khảo: Mục 2.5.1. Đạo hàm cấp cao (BG, tr.25).

The correct answer is: y′′=10(4−x)3

Select one:

a. x0=2y0

b. x0=−2y0

c. y0=2×0

d. y0=−2×0

Phản hồi

Đáp án đúng là: y0=2×0.

Vì: Từ 2 phương trình L′y=0,L′x=0 biểu diễn x,y qua λ từ đó rút được tỉ lệ giữa x và y: 3−6λx=0⇒x=12λ2−2λy=0⇒y=1λ⇒y=2x.

Tham khảo: Mục 5.3.2. Phương pháp nhân tử Lagrange (BG, tr.65).

The correct answer is: y0=2×0

Giả sử hàm sản xuất ngắn hạn của một doanh nghiệp là Q=30L2−−√3 . Giá trị sản phẩm hiện vật cận biên của lao động tại L = 27 là:

Select one:

a. 20/27

b. 902–√3

c. 270

d. 20/3

Phản hồi

Đáp án đúng là 203.

Vì: Q′=30.23L√3=20L√3⇒Q′(27)=203

Tham khảo: Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36).

The correct answer is: 20/3

Tích phân

I=∫π20(esinx+cosx).cosxdx.

có giá trị là:

Select one:

a. e+π4−1

b. e+π4+1

c. e−π4+1

d. e+π4+2

Phản hồi

Đáp án đúng là: e+π4−1.

Vì: I=∫π/20esinxcosxdx+∫π/20cos2xdx.

Tích phân đầu ta sử dụng tính bất biến, tích phân sau ta sử dụng phương pháp khai triển:

I=(esinx)∣∣π/20+12∫π/20(1+cos2x)dx.

I=e−1+[12(x+12sin2x)]∣∣π/20=e−1+π4.

Tham khảo: Mục 7.2. Các tính chất cơ bản của tích phân xác định (BG, tr. 87).

The correct answer is: e+π4−1

Kết quả đúng của tích phân: I=∫(x2+x+1).lnx.dx

Select one:

a. (x33+x22+x)⋅lnx−(x39+x24+x)+C

b. (x33−x22+x)⋅lnx+(x39+x24+x)+C

c. (x33−x22−x)⋅lnx+(x39+x24+x)+C

d. (x33+x22+x)⋅lnx+(x39+x24+x)+C

Phản hồi

The correct answer is: (x33+x22+x)⋅lnx−(x39+x24+x)+C

Giả sử hàm chi phí của một doanh nghiệp là TC=Q3−3Q+1 . Chi phí cận biên tại mức sản lượng Q = 3 là:

Select one:

a. 19

b. 25

c. 20

d. 24

Phản hồi

Đáp án đúng là: 24.

Vì: TC′=3Q2−3 ⇒ TC′(3)=24.

Tham khảo: Mục 3.3.1.1. Đạo hàm và giá trị cận biên trong kinh tế (BG, tr.36).

The correct answer is: 24

Theo quy luật lợi ích cận biên giảm dần, hàm sản xuất Q=f(K,L) sẽ phải thỏa mãn điều kiện:

Select one:

a. Q′′KK≤0;Q′′KL≤0, ∀K,L>0

b. Q′′LK≤0;Q′′KL≤0, ∀K,L>0

c. Q′′KK≤0;Q′′LL≥0, ∀K,L>0

d. Q′′KK≤0;Q′′LL≤0, ∀K,L>0

Phản hồi

Đáp án đúng là: Q′′KK≤0;Q′′LL≤0, ∀K,L>0

Vì: Theo quy luật lợi ích cận biên giảm dần các đạo hàm riêng cấp 2 theo cùng 1 biến số phải âm.

Tham khảo: Mục 4. 7. 2. Đạo hàm riêng cấp 2 và quy luật lợi ích cận biên giảm dần (BG, tr. 55).

The correct answer is: Q′′KK≤0;Q′′LL≤0, ∀K,L>0

Cho hàm số y=x.ln2x. Số điểm dừng của hàm số là:

Select one:

a. 1

b. 2

c. 3

d. 4

Phản hồi

Đáp án đúng là: 1.

Vì: y′=ln2x+1 Giải y′=0 ta được y′=0 ⇒ ln2x+1=0 ⇔ ln2x=−1 ⇔ 2x=e(−1) ⇔ x=1/2e → Hàm số có 1 điểm dừng.

Tham khảo: Mục 3.2. Tìm các điểm cực trị của hàm số (BG, tr.33).

The correct answer is: 1

Xét hàm số hai biến số w=f(x,y). Ký hiệu: D=∣∣∣a11a21a12a22∣∣∣=a11.a22−a12.a21 với a11,a12,a21,a22 lần lượt là giá trị của các đạo hàm riêng cấp 2 w′′xx,w′′xy,w′′yx,w′′yy tính tại điểm dừng M0(x0,y0). Khi đó nếu D<0 thì theo điều kiện đủ của cực trị, điểm M0(x0,y0):

Select one:

a. là điểm cực đại của hàm số.

b. là điểm cực tiểu của hàm số.

c. không là điểm cực trị của hàm số.

d. là điểm cực đại hoặc điểm cực tiểu của hàm số tùy theo dấu của a11.

Phản hồi

Đáp án đúng là: không là điểm cực trị của hàm số.

Vì: Theo điều kiện đủ của cực trị.

Tham khảo: Mục 5.1.3. Điều kiện đủ của cực trị (BG, tr.60).

The correct answer is: không là điểm cực trị của hàm số.

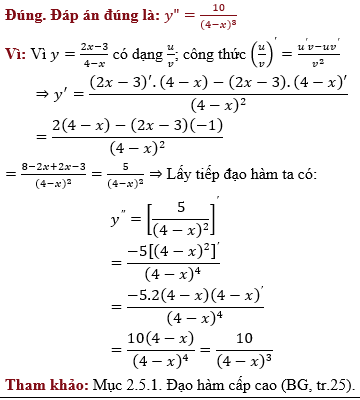
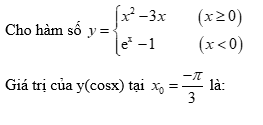
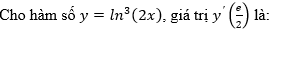
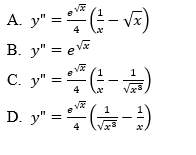
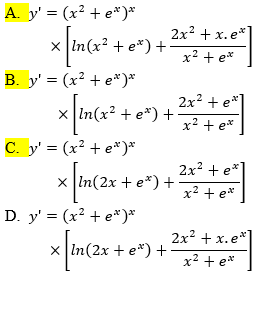
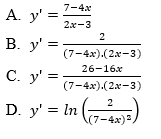
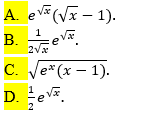
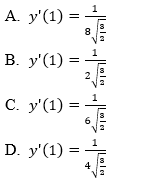
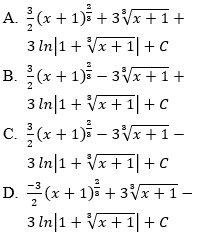
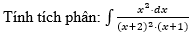
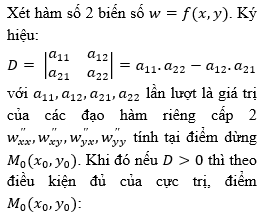
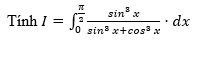
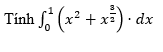
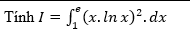
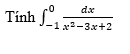
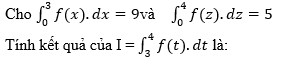
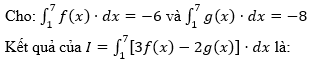
Trả lời Hủy

Chuyên mục

Toán cho các nhà kinh tế 1 (3TC)

Bài viết liên quan

Trả lời Hủy