Toán cho các nhà kinh tế 1 (2TC)
Để được nhận bản đầy đủ liên hệ TẠI ĐÂY
Cho véc tơ
X=(-3, 3, 2, 2) – 3(2, -2, 1)
-2(1, 2, 5, -2)
Thành phần thứ nhất của X có giá trị là:
- 10
- 10
- -11
Đáp án đúng là -11
Cho véctơ X1,X2,X3 và X thỏa mãn
X1 = (-3. 3, 2, 2)
X2 =(2, -2, -3, 1)
X3=(1, 2, 5, -2)
Thành phần thứ tư của X có giá trị là
- . −4
- . 5
- . −5
- . 4
Đáp án đúng là: -5
Cho véctơ X1,X2,X3 và X thỏa mãn
X1 = (-3 3 2 2)
X2 =(2 -2 -3 1)
X3=(1 2 5 -2)
Thành phần thứ tư của X có giá trị là
- . 5/3
- . −4/3
- . 4/3
- . −5/3
Đáp án đúng là: 5/3
Cho Véctơ
X=3m(-3 3 2 2)+2(2 -2 -3 1)
-3m(1 2 5 -2)
Thành phần thứ nhất của X có giá trị là:
- . 6 – 12m
- . 4 – 10m
- . 4 – 12m
- . 6 −10m
Đáp án đúng là: 4 – 12m
Cho Véctơ X=2(2, -3) -5 (3, 2) Thành phần thứ hai của X có giá trị là:
- . −16
- . –14
- . −12
- . −10
Đáp án đúng là: -16
Cho Véctơ
X1= (3,2)
X2 = (-3, -5)
X3= (-3, 4)
Giải sử X=a.X1+b.X2
Số a có giái trị là:
- . 0
- . −3
- . −1
- . −2
Đáp án đúng là: -3
Cho véctơ
X1=(-3,1)
X2=(2,4)
X=(2,-3)
X1, X2 đã cho là một cơ sở của R2. Tọa độ của X trong cơ sở đó có thành phần thứu hai là:
- . −1/4
- . −1/2
- . ½
- . 1/4
Đáp án đúng là: -1/2
Cho các véctơ: Nếu X1, X2, X3 là một cơ
Sở của R3. Khi đó, một véctơ X bất kỳ
Của R3 thì:
- X biểu diễn tuyến tính duy nhất qua X_1,X_2,X_3.
- X có vô số cách biểu diễn tuyến tính qua X_1,X_2,X_3.
- X không thể biểu diễn tuyến tính qua X_1,X_2,X_3.
- X có thể biểu diễn tuyến tính qua X_1,X_2,X_3.
Đáp án đúng là: X biểu diễn tuyến tính duy nhất qua X_1,X_2,X_3.
Cho các véctơ:
X1 = (-3,1)
X2= (2,4)
X = (2, -3)
Giả sử X=a.X1+b.X2
Số a có giái trị là:
- ½
- -1
- 1
- -1/2
Đáp án đúng là: -1
Nghiệm của hệ phương trình tuyến tính n ẩn là bộ n số có thứ tự thỏa mãn:
Select one:
a. . một vài phương trình trong hệ.
b. . phương trình đầu trong hệ.
c. . tất cả các phương trình trong hệ.
d. . ít nhất 1 phương trình trong hệ.
Phản hồi
Đúng. Đáp án đúng là: tất cả các phương trình trong hệ. Vì: Nghiệm của hệ phương trình tuyến tính n ẩn là bộ n số có thứ tự thỏa mãn tất cả các phương trình trong hệ. Tham khảo: Mục 1.1.1 Các khái niệm cơ bản (BG, tr.3).
The correct answer is: . tất cả các phương trình trong hệ.
Tổng của 2 véctơ 3 chiều là một:
Select one:
a. véctơ 6 chiều.
b. véctơ 3 chiều.
c. véctơ 2 chiều.
d. số thực.
Phản hồi
Đáp án đúng là: véctơ 3 chiều. Vì: Theo định nghĩa tổng của 2 véctơ n chiều là một véctơ n chiều. Tham khảo: Mục 1.2.2. Các phép toán vectơ (BG, tr.13).
The correct answer is: véctơ 3 chiều.
Cho vectơ:
X=5(-3 3 2 2)- 3m(2 -2 -3 1) – 2m(1 2 5 -2)
Thành phần thứ 2 của X có giá trị là:
Select one:
a. . 15 – 2m
b. . 13 + 2m
c. . 13 −2m
d. . 15 + 2m
Phản hồi
Đúng. Đáp án đúng là: 15 + 2m Vì: x_2=15+6m-4m=15+2m Tham khảo: Mục 1.2.2. Các phép toán vectơ (BG, tr.13).
The correct answer is: . 15 + 2m
Một hệ phương trình tuyến tính thuần nhất với 2 phương trình 3 ẩn luôn luôn có:
Select one:
a. . 3 nghiệm.
b. . 2 nghiệm.
c. . vô số nghiệm.
d. . vô nghiệm.
Phản hồi
Đúng. Đáp án đúng là: vô số nghiệm. Vì: Một hệ phương trình tuyến tính thuần nhất với 2 phương trình 3 ẩn thì quá trình biến đổi khử ẩn luôn kết thúc ở dạng hình thang nên có vô số nghiệm. Tham khảo: Mục 1.1. Hệ phương trình tuyến tính (BG, tr.3).
The correct answer is: . vô số nghiệm.
Cho vectơ:
X=(m, -3, 3, 2)- 3(2, -2m, -3, 1) – 2(1 2 5 -2)
Thành phần thứ nhất của X có giá trị là:
C21.PNG
Select one:
a. . m+6
b. . m+8
c. . m+2
d. . m+4
Phản hồi
Đúng. Đáp án đúng là: m + 4 Vì: x_1=m+6-2=m+4 Tham khảo: Mục 1.2.2. Các phép toán vectơ (BG, tr.13).
The correct answer is: . m+4
Cho các vectơ: X1,X2,X3 và X thỏa mãn:
X1 = (-3, 3, 2, 2)
X2 = (2, -2, -3, 1)
X3 = (1, 2, 5, -2)
-3X + 2X1 – 4 X2 =X3
Thành phần thứ nhất của X có giá trị là:
Select one:
a. . −5
b. . −4
c. . 5
d. . 4
Phản hồi
The correct answer is: . −5
Hai hệ phương trình tuyến tính với ẩn số như nhau và số phương trình khác nhau nhưng cùng vô nghiệm thì:
Select one:
a. . tương đương.
b. . có thể không tương đương.
c. . không tương đương.
d. . nếu số phương trình bằng số ẩn thì không tương đương.
Phản hồi
Đúng. Đáp án đúng là: tương đương. Vì: Hai hệ phương trình tuyến tính được gọi là tương đương nếu chúng có cùng ẩn số và tập hợp nghiệm bằng nhau. Tham khảo: Mục 1.1.1 Các khái niệm cơ bản (BG, tr.3).
The correct answer is: . tương đương.
Cho các vectơ:
X1 = (3,1)
X2 = (-2,4)
X =(-3,4)
Giả sử X= a.X1 + b.X2
Số a có giá trị là:
C53.PNG
Select one:
a. . −2/7
b. . −3/7
c. . 3/7
d. . 2/7
Phản hồi
Đúng. Đáp án đúng là: −2/7 Vì: Giải hệ phương trình tuyến tính 2 ẩn a, b có ma trận mở rộng nhận X1, X2, X lần lượt là các cột. Kết quả: (a,b)=[-2/7 15/14] Tham khảo: Mục 2.1.3. Dạng vectơ của hệ phương trình tuyến tính (BG, tr.20).
The correct answer is: . −2/7
Cho các vectơ:
X1 = (-2,3,-2,-4)
X2 = (3,-m,-2,1)
X = (2,-1,3,5)
Để ba vectơ đó phụ thuộc tuyến tính thì giá trị của m là:
Select one:
a. . 29/2
b. . 19/2
c. . −19/2
d. . −29/2
Phản hồi
Đúng. Đáp án đúng là: 29/2 Vì: Xét hệ phương trình thuần nhất có ma trận hệ số nhận các véctơ cột trên làm các cột theo thứ tự tương ứng. Biến đổi trên ma trận đó. Hệ vectơ trên phụ thuộc tuyến tính khi và chỉ khi hệ phương trình thuần nhất vô số nghiệm. Hệ phương trình đó có vô số nghiệm khi và chỉ khi: m ≠ 29/2 Tham khảo: Mục 2.2.2. Xét sự phụ thuộc tuyến tính của một hệ vectơ (BG, tr.23).
The correct answer is: . 29/2
Cho các vectơ:
X1 = (-3,1)
X2 = (2,4)
X =(2,-3)
X1, X2 đã cho là một cơ sở của R2. Tọa độ của X trong cơ sở đó có thành phần thứ hai là:
Select one:
a. . 1/2
b. . 1/4
c. . −1/4
d. . −1/2
Phản hồi
The correct answer is: . −1/2
Cho các vectơ:
X1 = (-3,1,2)
X2 = (2,-3,-2)
X3 = (3,4,2)
X =(2,1,-3)
X1, X2, X3 đã cho là một cơ sở của R3. Tọa độ của X trong cơ sở đó có thành phần thứ nhất là:
Select one:
a. . −19/6
b. . –5/2
c. . −7/2
d. . –5/6
Phản hồi
The correct answer is: . −19/6
Cho các vectơ:
X1 = (3,1,5)
X2 = (2,3,12)
X3 = (-4,-2,3)
X =(-3,1,3)
Giả sử X=a.X1+b.X2+c.X3 số a có giá trị là:
Select one:
a. . −3/59
b. . −1/59
c. . 3/59
d. . 1/59
Phản hồi
The correct answer is: . 1/59
C61.PNG
Select one:
a. . 59/40
b. . 59/60
c. . 49/40
d. . 49/60
Phản hồi
The correct answer is: . 49/60
Select one:
a. . -5/7
b. . 5/7
c. . 10/7
d. . -10/7
Phản hồi
Đúng. Đáp án đúng là: 10/7 Vì: Giải hệ phương trình tuyến tính 2 ẩn a, b có ma trận mở rộng nhận X1, X2, X lần lượt là các cột. Kết quả: (a, b)= [10/7 9/14] Tham khảo: Mục 2.1.3. Dạng vectơ của hệ phương trình tuyến tính (BG, tr.20).
The correct answer is: . 10/7
Cho các vectơ:
X1 = (3,1)
X2 = (-2,4)
X =(3,-4)
X1, X2 đã cho là một cơ sở của R2. Tọa độ của X trong cơ sở đó có thành phần thứ hai là:
Select one:
a. . 2/14
b. . 15/14
c. . −2/7
d. . −15/7
Phản hồi
The correct answer is: . 15/14
C44
Select one:
a. m≠0
b. Không tồn tại m.
c. m≠2
d. m≠1
Phản hồi
Đúng. Đáp án đúng là: m≠0 Vì: Hiển nhiên đây là hệ 3 véc tơ 3 chiều độc lập tuyến tính ↔m≠0. Tham khảo: Mục 2.3.1. Khái niệm cơ sở của không gian vectơ n chiều (BG, tr.25).
The correct answer is: m≠0
C64.PNG
Select one:
a. . −1/2
b. . 4/3
c. . 1/2
d. . −4/3
Phản hồi
The correct answer is: . −4/3
Cho hệ phương trình tuyến tính 3 phương trình 3 ẩn số, trường hợp nào sau đây không thể xảy ra?
Select one:
a. . Vô số nghiệm.
b. . Một nghiệm duy nhất.
c. . Vô nghiệm.
d. . Ba nghiệm.
Phản hồi
Đúng. Đáp án đúng là: Ba nghiệm. Vì:Một hệ phương trình tuyến tính chỉ có thể xảy ra các trường hợp về nghiệm: Một nghiệm duy nhất, vô số nghiệm, vô nghiệm. Tham khảo: Mục 1.1. Hệ phương trình tuyến tính (BG, tr.3).
The correct answer is: . Ba nghiệm.
Cho véctơ X=2(2,-3)-5(3,2)Thành phần thứ hai của X có giá trị là:
Select one:
a. . −10
b. . –14
c. . −12
d. . −16
Phản hồi
Đúng. Đáp án đúng là: −16 Vì: x_2=-6-10=-16 Tham khảo: Mục 1.2.2. Các phép toán vectơ (BG, tr.13).
The correct answer is: . −16
Hai hệ phương trình tuyến tính với số ẩn khác nhau nhưng cùng vô nghiệm thì:
Select one:
a. . không tương đương.
b. . có thể tương đương.
c. . nếu số phương trình bằng số ẩn thì tương đương.
d. . tương đương.
Phản hồi
Đúng. Đáp án đúng là: không tương đương. Vì: Hai hệ phương trình tuyến tính được gọi là tương đương nếu chúng có cùng ẩn số và tập hợp nghiệm bằng nhau. Tham khảo: Mục 1.1.1 Các khái niệm cơ bản (BG, tr.3).
The correct answer is: . không tương đương.
Trong một hệ phương trình tuyến tính bất kỳ:
Select one:
a. . phải có nhiều hơn 2 ẩn ở dạng bậc nhất.
b. . phải có ít nhất một ẩn ở dạng bậc nhất.
c. . tất cả các ẩn ở dạng bậc nhất.
d. . không có ẩn nào ở dạng bậc nhất.
Phản hồi
Đáp án đúng là: tất cả các ẩn ở dạng bậc nhất. Vì: Theo định nghĩa hệ phương trình tuyến tính. Tham khảo: Mục 1.1.1 Các khái niệm cơ bản (BG, tr.3).
The correct answer is: . tất cả các ẩn ở dạng bậc nhất.
Select one:
a. . 3m − 7
b. . 3m − 5
c. . 4m − 5
d. . 4m − 7
Phản hồi
Đúng. Đáp án đúng là: 4m – 7 Vì: x_2=-9+4m+2=4m-7 Tham khảo: Mục 1.2.2. Các phép toán vectơ (BG, tr.13).
The correct answer is: . 4m − 7
Select one:
a. X biểu diễn tuyến tính duy nhất qua X_1,X_2,X_3.
b. X không thể biểu diễn tuyến tính qua X_1,X_2,X_3.
c. X có thể biểu diễn tuyến tính qua X_1,X_2,X_3.
d. X có vô số cách biểu diễn tuyến tính qua X_1,X_2,X_3.
Phản hồi
Đúng. Đáp án đúng là: X không thể biểu diễn tuyến tính qua X_1,X_2,X_3. Vì: Ta thấy thành phần thứ 2 của X không thể biểu diễn qua thành phần thứ 2 của các véc tơ X_1,X_2,X_3. Tham khảo: Mục 2.1.1 Khái niệm tổ hợp tuyến tính (BG, tr.20) và mục 2.1.2 Phép biểu diễn tuyến tính (BG, tr.20).
The correct answer is: X không thể biểu diễn tuyến tính qua X_1,X_2,X_3.
C69.PNG
Select one:
a. . −15/7
b. . 15/14
c. . −2/7
d. . 2/14
Phản hồi
The correct answer is: . 15/14
C71.PNG
Select one:
a. . –5/2
b. . −7/2
c. . −19/6
d. . –5/6
Phản hồi
The correct answer is: . −19/6
Select one:
a. . 2/7
b. . −2/7
c. . 3/7
d. . −3/7
Phản hồi
Đúng. Đáp án đúng là: −2/7 Vì: Giải hệ phương trình tuyến tính 2 ẩn a, b có ma trận mở rộng nhận X1, X2, X lần lượt là các cột. Kết quả: (a,b)=[-2/7 15/14] Tham khảo: Mục 2.1.3. Dạng vectơ của hệ phương trình tuyến tính (BG, tr.20).
The correct answer is: . −2/7
C60
Select one:
a. . −9
b. . −8
c. . −10
d. . −11
Phản hồi
Đúng. Đáp án đúng là: −11 Vì: Giải hệ phương trình tuyến tính 3 ẩn a, b, c có ma trận mở rộng nhận X1, X2,X3, X lần lượt là các cột. Kết quả: (a, b, c)= [-11 -8 9] Tham khảo: Mục 2.1.3. Dạng vectơ của hệ phương trình tuyến tính (BG, tr.20).
The correct answer is: . −11
c83
Select one:
a. . 9
b. . 11
c. . 10
d. . 8
Phản hồi
Đúng. Đáp án đúng là: 11 Vì: a_31=6+5=11 Tham khảo: Mục 3.1. Các khái niệm cơ bản về ma trận (BG, tr.32) và mục 3.3. Các phép toán tuyến tính (BG, tr.35).
The correct answer is: . 11
c99
Select one:
a. Pa:D
b. Pa:B
c. Pa:C
d. Pa:A
Phản hồi
The correct answer is: Pa:B
c88
Select one:
a. Pa:D
b. Pa:A
c. Pa:C
d. Pa:B
Phản hồi
The correct answer is: Pa:B
c84
Select one:
a. . 11
b. . −11
c. . −7
d. . 7
Phản hồi
Đúng. Đáp án đúng là: −11 Vì: a_21=-9-2=-11 Tham khảo: Mục 3.1. Các khái niệm cơ bản về ma trận (BG, tr.32) và mục 3.3. Các phép toán tuyến tính (BG, tr.35).
The correct answer is: . −11
Cho ma trận A là kết quả của phép tính:
4⎡⎣⎢4433−32−124⎤⎦⎥−5⎡⎣⎢23−1−2−33142⎤⎦⎥
Phần tử nằm trên dòng 2 cột 3 của A là:
Select one:
a. 12
b. −12
c. −28
d. 28
Phản hồi
Đúng. Đáp án đúng là: −12 Vì: a23=8−20=−12. Tham khảo: Mục 3.1. Các khái niệm cơ bản về ma trận (BG, tr.32) và mục 3.3. Các phép toán tuyến tính (BG, tr.35).
The correct answer is: −12
c87
Select one:
a. . −7
b. . −11
c. . −5
d. . −13
Phản hồi
Đúng. Đáp án đúng là: −13 Vì: a_11=-9-4=-13 Tham khảo: Mục 3.1. Các khái niệm cơ bản về ma trận (BG, tr.32) và mục 3.3. Các phép toán tuyến tính (BG, tr.35).
The correct answer is: . −13




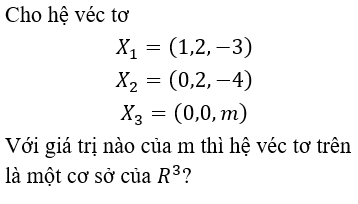
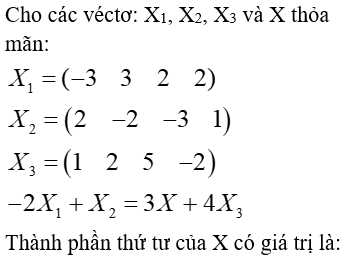
Trả lời